This ![]() represents the phase shift between input and output
voltages of the four-terminal network. According to
represents the phase shift between input and output
voltages of the four-terminal network. According to
![]() ,
the relative phase between
,
the relative phase between ![]() and
and
![]() is
the phase of the transfer function
is
the phase of the transfer function ![]() . So to find this phase
we write
. So to find this phase
we write
![]() in polar form,
in polar form,
![]() . The phase
. The phase ![]() of a complex number
of a complex number
![]() written as
written as
![]() is
is
![]() : it's inverse tangent of the imaginary part over
the real part. For the
: it's inverse tangent of the imaginary part over
the real part. For the ![]() network,
network,
![]() . This can be rewritten
(multiply top and bottom by
. This can be rewritten
(multiply top and bottom by
![]() ) as
) as
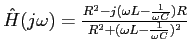 . Hence, the phase
shift for the network is
. Hence, the phase
shift for the network is
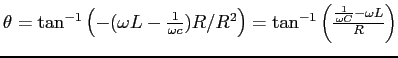 . We'll see lots of examples like this,
so work through the algebra if you are uncomfortable with it.
. We'll see lots of examples like this,
so work through the algebra if you are uncomfortable with it.