Damped Oscillation

So far, all the oscillators we've treated are ideal. There is no friction or damping. In the real world, of course, things always damp down. You have to keep pushing the kid on the swing or they slowly come to rest. Your car doesn't keep bouncing after going through a pothole in the road. Buildings and bridges, clocks and kids, real oscillators all have damping.

Damping forces can be very complicated. There is kinetic friction, which tends to be independent of speed. There are various fluid drag forces, which tend to depend on speed, but in a sometimes complicated way. There may be other forces that we haven't studied yet that contribute to damping. So in order to get beyond a very qualitative description of damping, we're going to have to specify a form for the damping force (ideally one we can work with, i.e. integrate).

We'll pick the simplest possible one:

$$F_d = - b v$$ (84)

($b$ is called the damping constant or damping coefficient) which is typical of an object being damped by a fluid at relatively low speeds. With this form we can get an exact solution to the differential equation easily (good), get a preview of a solution we'll need next semester to study LRC circuits (better), and get a very nice qualitative picture of damping besides (best).

We proceed with Newton's second law for a mass $m$ on a spring with spring constant $k$ and a damping force $-b v$:

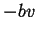$$F = -k x - b v = m a = m \frac{d^2x}{dt^2}$$ (85)

Again, simple manipulation leads to:

$$\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt} + \frac{k}{m} x = 0$$ (86)

which is standard form.

Again, it looks like a function that is proportional to its own first derivative is called for (and in this case this excludes sine and cosine as possibilities). We guess $x(t) = x_0 e^{\alpha t}$ as before, substitute, cancel out the common $x(t) \ne 0$ and get the characteristic:

$$\alpha^2 + \frac{b}{m} \alpha + \frac{k}{m} = 0$$ (87)

This is pretty easy, actually - each derivative just brings down an $\alpha$.

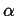To solve for 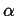$\alpha$ we have to use the dread quadratic formula:

$$\alpha = \frac{\frac{-b}{m} \pm \sqrt{\frac{b^2}{m^2} - \frac{4k}{m}}}{2}$$ (88)

This isn't quite where we want it. We simplify the first term, factor a $-4k/m$ out from under the radical (where it becomes $i\omega_0$, where $\omega_0 = \sqrt{k/m}$ is the frequency of the undamped oscillator with the same mass and spring constant) and get:

$$\alpha = \frac{-b}{2m} \pm i\omega_0 \sqrt{1 - \frac{b^2}{4km}}$$ (89)

Again, there are two solutions, for example:

$$x_{\pm}(t) = X_{0\pm}e^{\frac{-b}{2m}t} e^{\pm i\omega't}$$ (90)

where

$$\omega' = \omega_0 \sqrt{1 - \frac{b^2}{4km}}$$ (91)

Again, we can take the real part of their sum and get:

$$x_{\pm}(t) = X_0 e^{\frac{-b}{2m}t} \cos(\omega' t + \phi)$$ (92)

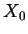where $X_0$ is the real initial amplitude and $\phi$ determines the relative phase of the oscillator.