The Physical Pendulum

In the treatment of the ordinary pendulum above, we just used Newton's Second Law directly to get the equation of motion. This was possible only because we could neglect the mass of the string and because we could treat the mass like a point mass at its end.

However, real grandfather clocks often have a large, massive pendulum like the one above - a long massive rod (of length $L$ and mass $m_L$) with a large round disk (of radius $R$ and mass $M_R$) at the end. The round weight rotates through an angle of $2\theta_0$ in each oscillation, so it has angular momemtum. Newton's Law for forces no longer suffices. We must use torque and the moment of inertia to obtain the frequency of the oscillator.

To do this we go through the same steps (more or less) that we did for the regular pendulum. First we compute the net gravitational torque on the system at an arbitrary (small) angle $\theta$:

$$\tau = -\left(\frac{L}{2} m_L g + L M_R g\right)\sin(\theta)$$ (76)

(The - sign is there because the torque opposes the angular displacement from equilibrium.)

Next we set this equal to $I\alpha$, where $I$ is the total moment of inertia for the system about the pivot of the pendulum and simplify:

$$\tau = -\left(\frac{L}{2} m_L g + L M_R g \right)\sin(\theta) = I \alpha = I \frac{d^2\theta}{dt^2}$$ (77)

$$I \frac{d^2\theta}{dt^2} + \left(\frac{L}{2} m_L g + L M_R g \right)\sin(\theta) = 0$$ (78)

and make the small angle approximation to get:

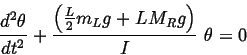$$\frac{d^2\theta}{dt^2} + \frac{\left(\frac{L}{2} m_L g + L M_R g \right)}{I} \theta = 0$$ (79)

Note that for this problem:

$$I = \frac{1}{12}m_L L^2 + \frac{1}{2} M_R R^2 + M_R L^2$$ (80)

(the moment of inertia of the rod plus the moment of inertial of the disk rotating about a parallel axis a distance $L$ away from its center of mass). From this we can read off the angular frequency:

$$\omega^2 = \frac{4\pi^2}{T} = \frac{\left(\frac{L}{2} m_L g + L M_R g \right)}{I}$$ (81)

With $\omega$ in hand, we know everything. For example:

$$\theta(t) = \theta_0 \cos(\omega t + \phi)$$ (82)

gives us the angular trajectory. We can easily solve for the period $T$, the frequency $f = 1/T$, the spatial or angular velocity, or whatever we like.

Note that the energy of this sort of pendulum can be tricky. Obviously its potential energy is easy enough - it depends on the elevation of the center of masses of the rod and the disk. The kinetic energy, however, is:

$$K = \frac{1}{2}I \left(\frac{d^2\theta}{dt^2}\right)^2$$ (83)

where I do not write $\frac{1}{2} I \omega^2$ as usual because it confuses $\omega$ (the angular frequency of the oscillator, roughly contant) and $\omega(t)$ (the angular velocity of the pendulum bob, which varies between 0 and some maximum value in every cycle).