


Next: Properties of Spherical Bessel
Up: Radiation
Previous: The Far Zone
Contents
Recall as you read this that and in addition to the
treatment of this available in Jackson, chapters 2, 3, 6, and 8 of Wyld,
and doubtless Arfkin, Morse and Feshback, and probably six other sources
if you look. Very important stuff, can't know it too well.
Recall from above the Homogeneous Helmholtz Equation (HHE):
 |
(13.12) |
We assume that13.6:
 |
(13.13) |
We reduce the HHE with this assumption to the radial differential
equation
![$\displaystyle \left[ \frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr} + k^2 - \frac{\ell(\ell + 1)}{r^2} \right] f_\ell (r) = 0.$](img957.png) |
(13.14) |
If we substitute
 |
(13.15) |
we transform this into an equation for
 ,
,
![$\displaystyle \left[ \frac{d^2}{dr^2} + \frac{1}{r} \frac{d}{dr} + k^2 - \frac{(\ell + \frac{1}{2})^2}{r^2} \right] u_\ell (r) = 0.$](img960.png) |
(13.16) |
The is Bessel's differential equation. See Wyld, (2-6) or
Jackson in various places (see key on back inside cover) for more
detail. Or your own favorite Math Physics book.
Two linearly independent solutions on  minus the origin to this
radial DE are:
minus the origin to this
radial DE are:
the spherical bessel function and spherical neumann
functions respectively. They are both real, and hence are stationary
in time (why?). The
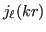 are regular (finite) at the
origin while the
are regular (finite) at the
origin while the
 are irregular (infinite) at the
origin. This is in exact analogy with the situation for the
homogeneous Laplace equation (which is a special case of this
solution).
are irregular (infinite) at the
origin. This is in exact analogy with the situation for the
homogeneous Laplace equation (which is a special case of this
solution).
The following is a MINIMAL table of their important properties.
A better table can be found in Wyld between chps. 6 and 7 and in Morse
and Feshbach (I can't remember which volume).
Subsections

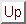


Next: Properties of Spherical Bessel
Up: Radiation
Previous: The Far Zone
Contents
Robert G. Brown
2017-07-11

![$\displaystyle \left[ \frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr} + k^2 - \frac{\ell(\ell + 1)}{r^2} \right] f_\ell (r) = 0.$](img957.png)

![$\displaystyle \left[ \frac{d^2}{dr^2} + \frac{1}{r} \frac{d}{dr} + k^2 - \frac{(\ell + \frac{1}{2})^2}{r^2} \right] u_\ell (r) = 0.$](img960.png)
![]() minus the origin to this
radial DE are:
minus the origin to this
radial DE are: