

Next: The Lowest Few Functions
Up: Properties of Spherical Bessel
Previous: Properties of Spherical Bessel
Contents
Let 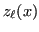 be either solution or a linear combination of the
two.
be either solution or a linear combination of the
two. 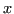 is a complex scalar independent variable (in practice,
is a complex scalar independent variable (in practice, 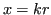 ). Then
). Then
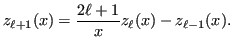 |
(13.19) |
This relation is stable for increasing  for
for
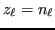 .
It is stable for decreasing
.
It is stable for decreasing  for
for
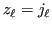 . For that
reason it is unstable in both directions for
. For that
reason it is unstable in both directions for
 (defined below). How would you make it? See Abramowitz and Stegun,
Handbook of Mathmatical Functions for discussion of recursive
algorithm and definition of power series expansions.
(defined below). How would you make it? See Abramowitz and Stegun,
Handbook of Mathmatical Functions for discussion of recursive
algorithm and definition of power series expansions.
Robert G. Brown
2017-07-11
![]() be either solution or a linear combination of the
two.
be either solution or a linear combination of the
two. ![]() is a complex scalar independent variable (in practice,
is a complex scalar independent variable (in practice, ![]() ). Then
). Then