Why does the low-pass filter act as an integrator?

The low-pass filter acts as an integrator at high frequencies, such that 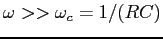$\omega >> \omega_c = 1/(RC)$. You can look at this in two ways:

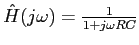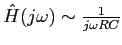• First, mathematically: the transfer function of the low-pass filter is $\hat{H}(j \omega) = \frac{1}{1+j\omega RC}$, and in the $\omega >> \omega_c$ limit this looks like $\hat{H}(j \omega) \sim \frac{1}{j\omega RC}$. Multiplying by 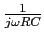$\frac{1}{j\omega RC}$ does exactly the same thing as integration (times a constant) for a sinusoidally-varying signal (or a superposition of sinusoidally-varying signals, which every periodic signal is by Fourier analysis): if $\hat{V}_{\rm in} = \hat{V} e^{j\omega t}$, then the integral is $\int \hat{V} e^{j\omega t}\ = \frac{1}{j\omega} \hat{V} e^{j \omega t} = \frac{1}{j \omega} \hat{V}_{\rm in}$.

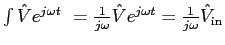• Second, thinking physically: the output is voltage across the capacitor, which is proportional to charge stored in the capacitor. At high frequency, with driving voltage rapidly flipping back and forth, you are always in mode where you have ``just started'' charging or discharging the capacitor, i.e., in a mode ``right after flipping the switch''. In this situation, at each instant, charge added to the capacitor in a given time interval is proportional to 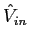$\hat{V}_{in}$ at that time, and so total charge stored will be the sum of charge and proportional to integral of the voltage.