Conversion of Asteroid
Proper Motion to Distance from the Sun
version 1.2
2/9/99
Goal: given the location of asteroid
in the sky (in terms of right ascension and declination), the date for
which the location is known, and the proper motion of the asteroid, this
procedure will determine the radius of the asteroid's orbit (under the
assumptions operating below).
Assumptions:
1) the orbit of both earth and the
asteroid are circular
2) the orbit of the asteroid is
coplanar with the orbit of the earth
3) direction of the orbit revolution
of the asteroid is the same as that of earth
4) the asteroid orbit is larger
than that of the earth (aa > ae)
5) the sun is infinitely massive
(this simplifies Kepler's 3rd law)
6) the asteroid is at least 90
degrees in direction away from the sun as seen from
the earth, i.e.,
| 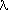 s -
s - 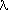 a
| > 90
a
| > 90
(this assumption
may be retracted in the next version)

definitions:
s, e, a
subscript symbols for sun, earth, asteroid
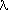 celestial longitude (angle measured eastward along the ecliptic from the
vernal
celestial longitude (angle measured eastward along the ecliptic from the
vernal
equinox)
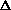 absolute value of the angle between directions to sun and asteroid, as
seen
absolute value of the angle between directions to sun and asteroid, as
seen
from earth; by definition = | 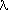 s
-
s
- 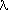 a |
a |
 angle between directions to earth and to sun, as seen from the asteroid
angle between directions to earth and to sun, as seen from the asteroid
 angle (as seen from the asteroid) between direction to earth and direction
of the
angle (as seen from the asteroid) between direction to earth and direction
of the
asteroid's orbital motion;
by definition,  = 90
-
= 90
-  (1)
(1)
 180 - the angle (as seen from earth) between direction to asteroid and
direction
180 - the angle (as seen from earth) between direction to asteroid and
direction
ofearth's orbital motion;
by definition,  =
= 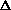 - 90
(2)
- 90
(2)
other orbital parameters
a orbital
radius
P orbital
period
v orbital
speed;by definition,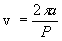 (3)
(3)
but Kepler's 3rd law requires that 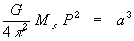 (4)
(4)
therefore, 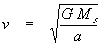 (5)
(5)
by the law of sines,  (6)
(6)
by the law of cosines,
aa2 = d2 + ae2
- 2 d ae cos 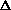 (7)
(7)
and
ae2 = aa2
+ d2 - 2 d aacos q
(8)
by definition, angular speed = 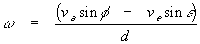 (9)
(9)
but , by (2), sin  = sin (
= sin ( 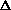 - 90) = - cos
- 90) = - cos 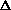 (10)
(10)
substituting (5) and
(10) into (9) gives,
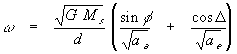 (11)
(11)
now use (6) to solve for 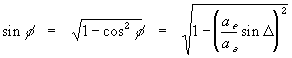 (12)
(12)
to obtain [by substituting
(12) into (11)]
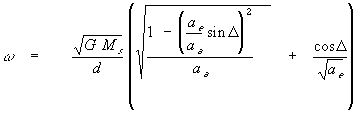 (13)
(13)
now use (7) to solve for d
via the quadratic formula,
 (14)
(14)
then,
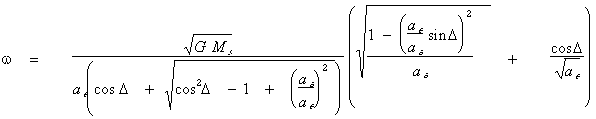 (15)
(15)
notice that the right side of the
equation has units the of 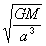
if numbers are now entered for Ms
and G, and if a is now expressed in units of au's (1 au = ae),
then
 (16)
(16)
the equation that must then be solved
for the unknown asteroid orbit radius x
(formerly called aa
) (which will come out in units of au's) is
 (17)
(17)
The absolute value (abs) is necessary
because only the magnitude of the proper motion is entered as w.
Remember that assumption (4) above requires that x > 1.
The most straightforward way
to solve this equation is graphically.
To determine the orbit size of an
asteroid, the following inputs are needed:
1) the celestial longitude of the
asteroid on the date that the image was taken; if the
right ascension
and declination of the
asteroid are known
go to the NED
Coordinate Calculator to
determine the celestial longitude of the
asteroid
(when you get there, select "equatorial" as your input
system and
select "ecliptic" for your output
system)
2) the celestial longitude of the
sun on the date that the image was taken; the date
that the image
wastaken can be used to calculate the celestial longitude;
to determine
the sun's right ascension and declination from the date of
the
image, try using any planetarium
program. e.g., TheSky
(I am trying to find a web link
for this step, but have been unsuccessful to date.)
again go to the NED
Coordinate Calculator to determine
the celestial longitude of the
sun from its rightascension
and declination
3) now that both celestial longitudes
are known, calculate 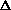 =
|
=
| 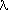 s -
s - 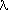 a
|
a
|
4) the proper motion of the asteroid
in units of radians/sec
if the
proper motion is known in arcsec/sec, then
 (radians/sec) =
(radians/sec) =  (arcsec/sec)
/ 206265
(arcsec/sec)
/ 206265
To solve equation (17) for
x
, you can
1) program your graphing calculator
or
2) go to Visual
Math For Java for a Java applet
that will solve the equation
PM - 1.991E-7*abs(sqrt((1-((sin(del))/x)^2)/x)+cos(del))/(cos(del)+sqrt((cos(del))^2-1+x^2))
where PM stands for the proper motion 
and del stands for the angle 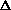 (which will need to be converted to radians)
(which will need to be converted to radians)
you can copy the above string and paste it into a dialog
box in a Java applet; don't forget to replace PM and del (3 times) by numbers!

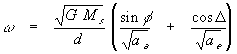 (11)
(11)
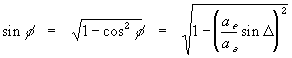 (12)
(12)
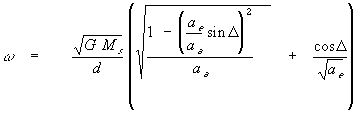 (13)
(13)
 (14)
(14)
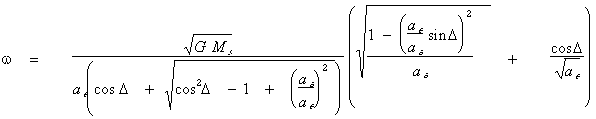 (15)
(15)
 (16)
(16)
 (17)
(17)