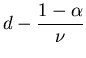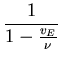Next: About this document ...
The Critical Scaling of the
Helicity Modulus of the O(3)
classical Heisenberg ferromagnet
Robert G. Brown
Acknowledgements: This work was done with my good friend and colleague,
Dr. Mikael Ciftan. We gratefully acknowledge the support of the Army
Research Office.
Model
Classical Heisenberg ferromagnet (CHF) (the  model on a
3
model on a
3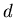 simple cubic lattice with periodic boundary conditions) in zero
external field:
simple cubic lattice with periodic boundary conditions) in zero
external field:
Goal
To compute and ``measure'' (with Monte Carlo) the critical exponents of
the model, in particular the critical exponent 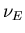 of the Helicity
Modulus
of the Helicity
Modulus 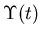 .
.
Methods
- Importance Sampling Monte Carlo (heat bath) ``with a twist'' to
get
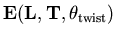 at high precision for
at high precision for
![$\bf L \in
[8,64...]$](img16.png) .
.
- Finite size scaling used to get critical exponents at
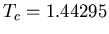 (accepted value,
(accepted value, 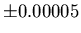 ).
).
- Helicity studied by freezing and twisting the (previously
periodic) boundary conditions in the (X,Y,1) plane.
Review of Theory
- Landau potential for a continuous ferromagnetic model is:
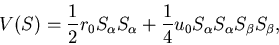 |
(1) |
where 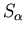 are the cartesian components of the coarse grain block
spins.
are the cartesian components of the coarse grain block
spins.
- Define the block spin
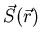 in terms of its mean
value (the order parameter) plus a fluctuation:
in terms of its mean
value (the order parameter) plus a fluctuation:
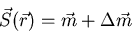 |
(2) |
- Further decompose the fluctuation into a longitudinal and
transverse piece:
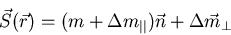 |
(3) |
- Derive the following general form for the free energy in terms of
the transverse coarse grained spin fluctuation gradient
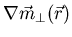 :
:
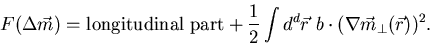 |
(4) |
(with phenomenological parameter 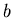 , the ``spin wave stiffness''.
, the ``spin wave stiffness''.
- One can relate a state of uniform twist angle to the gradient of
the transverse spin fluctuation via
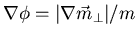 . Substituting and differentiating to find the free
energy density, one obtains the following two relations:
. Substituting and differentiating to find the free
energy density, one obtains the following two relations:
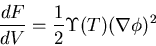 |
(5) |
with
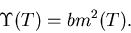 |
(6) |
- In Landau theory,
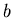 approximately constant so
approximately constant so
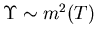 as
as 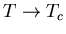 from below. In detailed treatment one gets
corrections:
from below. In detailed treatment one gets
corrections:
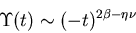 |
(7) |
- Finally, to use finite-size scaling theory (FSST) to extract the
critical exponent, we must substitute
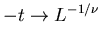 , or
, or
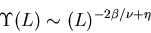 |
(8) |
In the last expression,
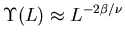 .
.
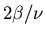 term from
term from 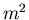 clearly dominant (
clearly dominant (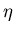 is very small,
is very small,
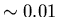 , for this model, while
, for this model, while
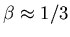 and
and
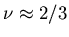 ). The helicity modulus should vanish sharply near
). The helicity modulus should vanish sharply near 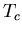 according to Landau theory.
according to Landau theory.
But...
We cannot directly measure the free energy density 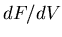 . We can directly measure the enthalpy density
. We can directly measure the enthalpy density 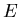 . Following an identical
argument:
. Following an identical
argument:
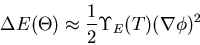 |
(9) |
where
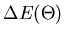 is the change in internal energy caused by
twisting the boundary conditions through the angle
is the change in internal energy caused by
twisting the boundary conditions through the angle
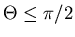 with either helicity. From this obvious substitutions yield:
with either helicity. From this obvious substitutions yield:
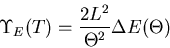 |
(10) |
With a page or two of algebra we can show that:
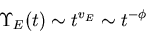 |
(11) |
with the critical exponent
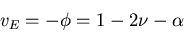 |
(12) |
This is what we wish to measure, in part to invert this equation
and deduce the values of 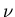 and
and 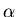 .
.
Note that as before, if we make the finite size scaling hypothesis we
will actually measure:
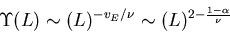 |
(13) |
or
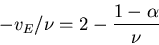 |
(14) |
The enthalpy helicity should thus diverge at 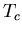 .
.
It is easy to show that:
where the second step uses ``hyperscaling'' (widely believed but by no
means proven for this model) to eliminate  for
for 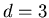 . With
this we can compute
. With
this we can compute 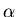 and
and 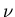 given
given 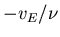 and possibly
check hyperscaling.
and possibly
check hyperscaling.
Measuring 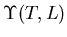 with Monte Carlo
with Monte Carlo
- Calculations were performed on several generations of ``brahma''
(our beowulf compute cluster, also ganesh and rama).
- Heat bath only (cluster method a bit difficult if boundary layers
are ``frozen'').
- Equilibrate
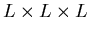 lattice with periodic boundary
conditions.
lattice with periodic boundary
conditions.
- ``Freeze'' (x,y,1) layer of spins.
- Rotate (x,y,1) spins through angle
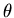 and store them in
(x,y,L+1) layer (replacing PBC's in z-direction with frozen twisted PBC's).
and store them in
(x,y,L+1) layer (replacing PBC's in z-direction with frozen twisted PBC's).
- Re-equilibrate only the (x,y,2) to (x,y,L) spins with the heat
bath (with PBC's in the x and y directions).
- Sample
- Repeat (easiest to restore PBC's, re-equilibrate, repeat).
- Sweep angles
![$\theta \in [0,\pi/2]$](img66.png) ,
, ![$L \in [8,48]$](img67.png) at
at 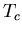 .
.
- Fit
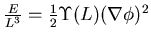 where
where
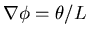 .
.
- Fit
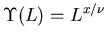
- Obtain
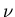 ,
, 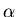 from hyperscaling.
from hyperscaling.
Results
Figure 1:
E per spin as function of interlayer twist angle 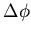 for
for 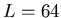 (in progress). This is fit to obtain the helicity.
(in progress). This is fit to obtain the helicity.
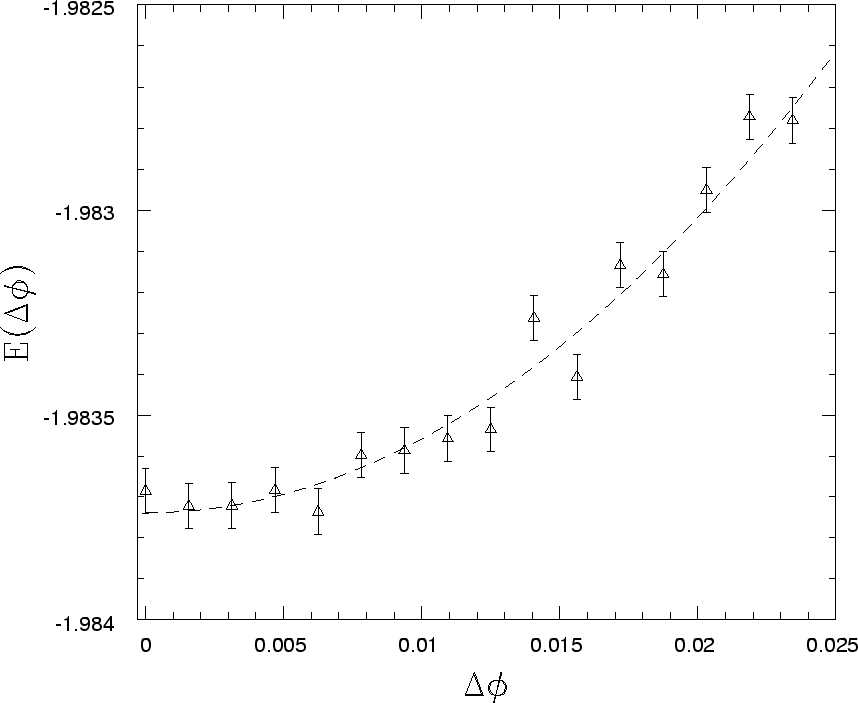 |
Figure 2:
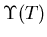 for
for 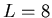 and
and 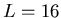 , evaluated at low
precision to get trend only.
, evaluated at low
precision to get trend only.
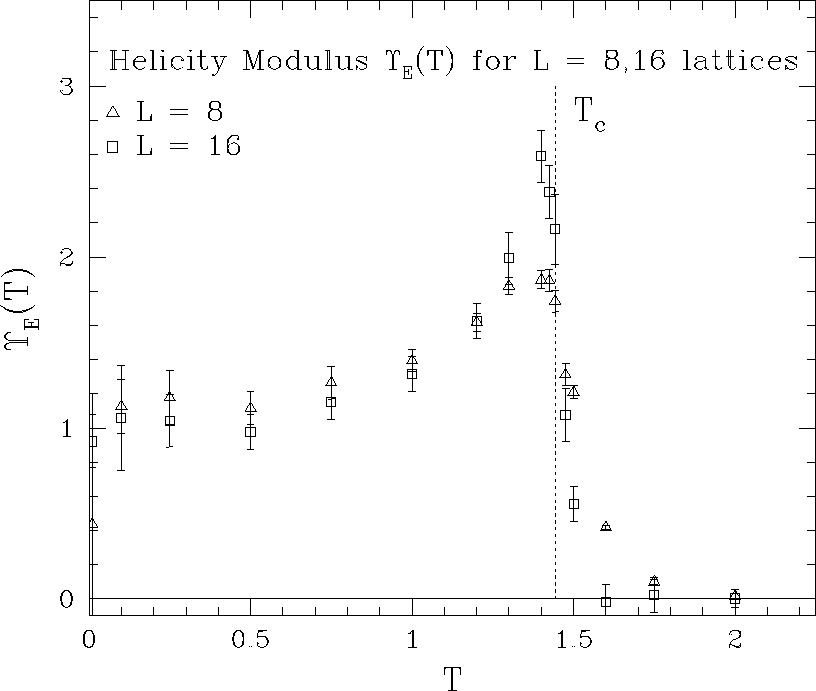 |
Figure 3:
The helicities for various 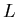 at
at 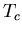 . The nonlinear least
squares fit of this yields
. The nonlinear least
squares fit of this yields
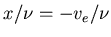 .
.
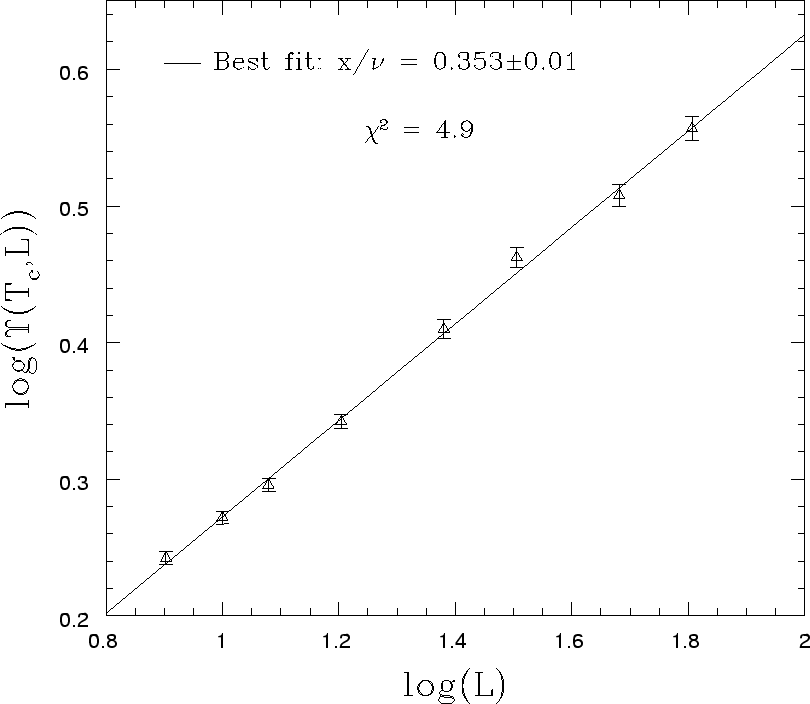 |
Best result to date:
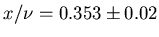
Conclusions
- The only direct measurement of this quantity to date.
-
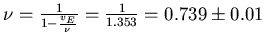 . This is quite large compared to most other Monte Carlo
results (which tend to yield
. This is quite large compared to most other Monte Carlo
results (which tend to yield
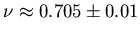 ) but is not
inconsistent with the most recent renormalization predictions.
) but is not
inconsistent with the most recent renormalization predictions.
- The hyperscaling relation itself then yields
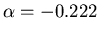 .
This is a weakly singular quantity and is very difficult to
measure. This is a major motivation of this work.
.
This is a weakly singular quantity and is very difficult to
measure. This is a major motivation of this work.
- For this particular talk, we emphasize that there are easily more
than 30 ``GFLOP-years'' of effort in this result (whatever you consider
a GFLOP to be). (32x400x3 = 38400) + (16x1300x2 = 41600) + (32x1600x1 =
51200) = 131.200 GHz-years, supercomputing indeed. Impossible without
the beowulf/cluster model.



Next: About this document ...
Robert G. Brown
2003-04-07


![]() .
.
![]() term from
term from ![]() clearly dominant (
clearly dominant (![]() is very small,
is very small,
![]() , for this model, while
, for this model, while
![]() and
and
![]() ). The helicity modulus should vanish sharply near
). The helicity modulus should vanish sharply near ![]() according to Landau theory.
according to Landau theory.
![]() . We can directly measure the enthalpy density
. We can directly measure the enthalpy density ![]() . Following an identical
argument:
. Following an identical
argument:
![]() and
and ![]() .
.
![]() .
.