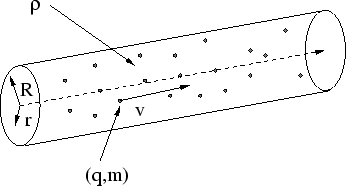
.

Beam Dynamics: Each part of this problem (a and b) will be graded separately. You do not need to get the first part right to do the second part, but obviously you need to get both parts right to get the extra credit.

A cylindrical beam of particles each with charge $q$ and mass $m$ has a uniform initial (charge) density $\rho$ and radius $R$. Each particle in the beam is initially travelling with velocity $v$ parallel to the beam's axis. We will discuss the stability of this beam by examining the forces on a particle travelling in the beam at a distance $r<R$ from the axis (the center of the cylinder).

a) Find the force on a particle at radius $r$ caused by the other particles in the beam. You will need to use Gauss's law to calculate the electric field at radius $r$. Describe your work, and do not skip steps; show that you understand Gauss's law. Make a sketch as needed. .