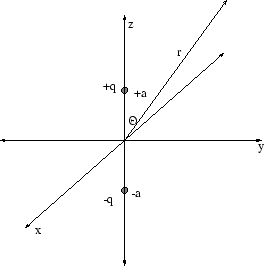

A point charge of ![]() is located at
is located at ![]() on the
on the ![]() -axis and a point
charge of
-axis and a point
charge of ![]() is located at
is located at ![]() .
.
(Note: Obviously, I really do want you to learn to do this one,
since I did a bunch of it in lecture and asked you to finish the rest on
your own. You derive a very fundamental result that will be useful to
you in the years to come....so much that I'll give two hints. One is
use the law of cosines to determine the distance from e.g. ![]() to the
point of observation in terms of
to the
point of observation in terms of ![]() ,
, ![]() , and
, and ![]() only. Second is
to use the binomial expansion to extract the leading order potential
term(s) for each charge and add them until you get the overall leading
order term that survives - the first term or two might well
cancel.)
only. Second is
to use the binomial expansion to extract the leading order potential
term(s) for each charge and add them until you get the overall leading
order term that survives - the first term or two might well
cancel.)