


Next: Zeroth Law of Thermodynamics
Up: Fluids
Previous: Fluids
Contents
A fluid in static equilibrium must support its own weight. If one
considers a small circular box of fluid with area  perpendicular to gravity and sides of thickness
perpendicular to gravity and sides of thickness  , the force on the
sides cancels due to symmetry. The force pushing down at the top of the
box is
, the force on the
sides cancels due to symmetry. The force pushing down at the top of the
box is 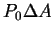 . The force pushing up from the bottom of the box
is
. The force pushing up from the bottom of the box
is
 . The weight of the fluid in the box is
. The weight of the fluid in the box is
 . Thus:
. Thus:
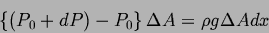 |
(213) |
or
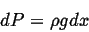 |
(214) |
If  is itself a function of pressure/depth (as occurs with e.g.
air) this can be a complicated expression to evaluate. For an
incompressible fluid such as water,
is itself a function of pressure/depth (as occurs with e.g.
air) this can be a complicated expression to evaluate. For an
incompressible fluid such as water,  is constant over rather large
variations in pressure. In that case, integration yields:
is constant over rather large
variations in pressure. In that case, integration yields:
 |
(215) |



Next: Zeroth Law of Thermodynamics
Up: Fluids
Previous: Fluids
Contents
Robert G. Brown
2004-04-12
![]() perpendicular to gravity and sides of thickness
perpendicular to gravity and sides of thickness ![]() , the force on the
sides cancels due to symmetry. The force pushing down at the top of the
box is
, the force on the
sides cancels due to symmetry. The force pushing down at the top of the
box is ![]() . The force pushing up from the bottom of the box
is
. The force pushing up from the bottom of the box
is
![]() . The weight of the fluid in the box is
. The weight of the fluid in the box is
![]() . Thus:
. Thus: