


Next: The Gravitational Field
Up: Gravity
Previous: Ellipses and Conic Sections
Contents
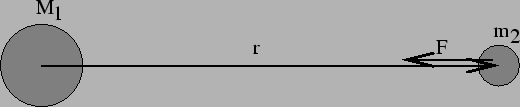
- Force of gravity acts on a line joining centers of masses.
- Force of gravity is attractive.
- Force of gravity is proportional to each mass.
- Force of gravity is inversely proportional to the distance
between the centers of the masses.
or,
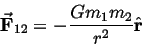 |
(4) |
where
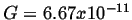 N-m
N-m /kg
/kg is the universal
gravitational constant.
is the universal
gravitational constant.
Kepler's first law follow from solving Newton's laws and the
equations of motion for this particular force law. This is a bit
difficult and beyond the scope of this course, although we will
show that circular orbits are one special solution that easily satisfy
Kepler's Laws.
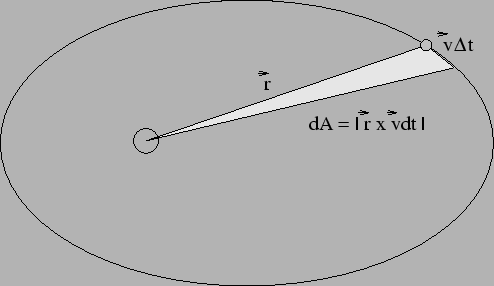
Kepler's Second Law is proven by observing that this force is radial,
and hence exerts no torque. Thus the angular momentum of a planet is
constant! That is,
or
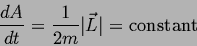 |
(7) |
(and Kepler's second law is proved for this force).
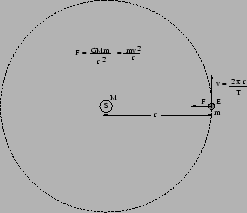
For a circular orbit, we can also prove Kepler's Third Law. The orbit
is circular, so we have a relation between  and
and 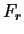 .
.
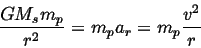 |
(8) |
so that
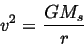 |
(9) |
But,  is related to
is related to  and the period
and the period  by:
by:
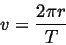 |
(10) |
so that
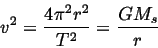 |
(11) |
Finally,
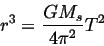 |
(12) |
and Kepler's third law is proved for circular orbits (and the constant
 evaluated for the solar system!).
evaluated for the solar system!).



Next: The Gravitational Field
Up: Gravity
Previous: Ellipses and Conic Sections
Contents
Robert G. Brown
2004-04-12

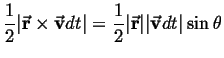
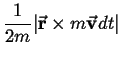
![]() and
and ![]() .
.