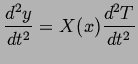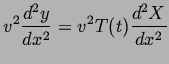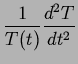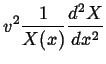


Next: Reflection of Waves
Up: Solutions to the Wave
Previous: Harmonic Waveforms Propagating to
Contents
The third special case of solutions to the wave equation is that of standing waves. They are especially apropos to waves on a string fixed
at one or both ends. There are two ways to find these solutions from
the solutions above. A harmonic wave travelling to the right and
hitting the end of the string (which is fixed), it has no choice but to
reflect. This is because the energy in the string cannot just
disappear, and if the end point is fixed no work can be done by it on
the peg to which it is attached. The reflected wave has to have the
same amplitude and frequency as the incoming wave. What does the sum of the incoming and reflected wave look like in this special case?
Suppose one adds two harmonic waves with equal amplitudes, the same
wavelengths and frequencies, but that are travelling in opposite
directions:
(where we give the standing wave the arbitrary amplitude  ). Since
all the solutions above are independent of the phase, a second useful
way to write stationary waves is:
). Since
all the solutions above are independent of the phase, a second useful
way to write stationary waves is:
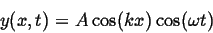 |
(124) |
Which of these one uses depends on the details of the boundary
conditions on the string.
In this solution a sinusoidal form oscillates harmonically up and down,
but the solution has some very important new properties. For one, it is
always zero when  for all possible
for all possible  :
:
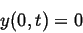 |
(125) |
For a given  there are certain other
there are certain other  positions where the
wave vanishes at all times. These positions are called nodes of
the wave. We see that there are nodes for any
positions where the
wave vanishes at all times. These positions are called nodes of
the wave. We see that there are nodes for any  such that:
such that:
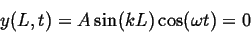 |
(126) |
which implies that:
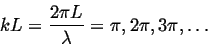 |
(127) |
or
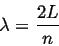 |
(128) |
for 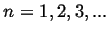
Only waves with these wavelengths and their associated frequencies
can persist on a string of length  fixed at both ends so that
fixed at both ends so that
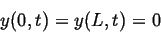 |
(129) |
(such as a guitar string or harp string). Superpositions of these waves
are what give guitar strings their particular tone.
It is also possible to stretch a string so that it is fixed at one end
but so that the other end is free to move - to slide up and
down without friction on a greased rod, for example. In this case,
instead of having a node at the free end (where the wave itself
vanishes), it is pretty easy to see that the slope of the wave at
the end has to vanish. This is because if the slope were not zero, the
terminating rod would be pulling up or down on the string, contradicting
our requirement that the rod be frictionless and not able to pull
the string up or down, only directly to the left or right due to
tension.
The slope of a sine wave is zero only when the sine wave itself is a
maximum or minimum, so that the wave on a string free at an end must
have an antinode (maximum magnitude of its amplitude) at the free
end. Using the same standing wave form we derived above, we see that:
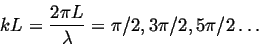 |
(130) |
for a string fixed at  and free at
and free at 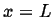 , or:
, or:
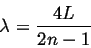 |
(131) |
for 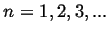
There is a second way to obtain the standing wave solutions that
particularly exhibits the relationship between waves and harmonic
oscillators. One assumes that the solution  can be written as
the product of a fuction in
can be written as
the product of a fuction in  alone and a second function in
alone and a second function in  alone:
alone:
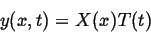 |
(132) |
If we substitute this into the differential equation and divide by
 we get:
we get:
where the last line follows because the second line equations a function
of  (only) to a function of
(only) to a function of  (only) so that both terms must equal
a constant. This is then the two equations:
(only) so that both terms must equal
a constant. This is then the two equations:
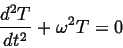 |
(136) |
and
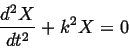 |
(137) |
(where we use 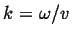 ).
).
From this we see that:
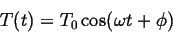 |
(138) |
and
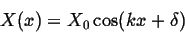 |
(139) |
so that the most general stationary solution can be written:
 |
(140) |



Next: Reflection of Waves
Up: Solutions to the Wave
Previous: Harmonic Waveforms Propagating to
Contents
Robert G. Brown
2004-04-12
![]() for all possible
for all possible ![]() :
:
![]() fixed at both ends so that
fixed at both ends so that
![]() can be written as
the product of a fuction in
can be written as
the product of a fuction in ![]() alone and a second function in
alone and a second function in ![]() alone:
alone: