


Next: Relations Involving
Up: Simple Harmonic Oscillation
Previous: Simple Harmonic Oscillation
Contents
We generally are interested in real part of  when studying
oscillating masses, so we'll stick to the following solution:
when studying
oscillating masses, so we'll stick to the following solution:
 |
(57) |
where 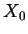 is called the amplitude of the oscillation and
is called the amplitude of the oscillation and  is called the phase of the oscillation. The amplitude tells you
how big the oscillation is, the phase tells you when the oscillator was
started relative to your clock (the one that reads
is called the phase of the oscillation. The amplitude tells you
how big the oscillation is, the phase tells you when the oscillator was
started relative to your clock (the one that reads  ). Note that we
could have used
). Note that we
could have used
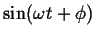 as well, or any of several other
forms, since
as well, or any of several other
forms, since
 . But you knew that.
. But you knew that.
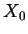 and
and  are two unknowns and have to be determined from the
initial conditions, the givens of the problem. They are basically
constants of integration just like
are two unknowns and have to be determined from the
initial conditions, the givens of the problem. They are basically
constants of integration just like  and
and  for the
one-dimensional constant acceleration problem. From this we can easily
see that:
for the
one-dimensional constant acceleration problem. From this we can easily
see that:
 |
(58) |
and
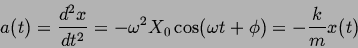 |
(59) |
(where the last relation proves the original differential equation).



Next: Relations Involving
Up: Simple Harmonic Oscillation
Previous: Simple Harmonic Oscillation
Contents
Robert G. Brown
2004-04-12
![]() and
and ![]() are two unknowns and have to be determined from the
initial conditions, the givens of the problem. They are basically
constants of integration just like
are two unknowns and have to be determined from the
initial conditions, the givens of the problem. They are basically
constants of integration just like ![]() and
and ![]() for the
one-dimensional constant acceleration problem. From this we can easily
see that:
for the
one-dimensional constant acceleration problem. From this we can easily
see that: