


Next: Relations between cosine, sine
Up: Math: Complex Numbers and
Previous: Math: Complex Numbers and
Contents
This is a very terse review of their most important properties. An
arbitrary complex number 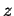 can be written as:
can be written as:
where
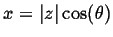 ,
,
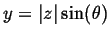 , and
, and
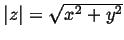 . All complex numbers can be written as a real amplitude
. All complex numbers can be written as a real amplitude
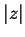 times a complex exponential form involving a phase angle. Again,
it is difficult to convey how incredibly useful this result is without
further study, but I commend it to your attention.
times a complex exponential form involving a phase angle. Again,
it is difficult to convey how incredibly useful this result is without
further study, but I commend it to your attention.
Robert G. Brown
2004-04-12