

We will work in one dimension (call it ![]() ) and will for the time being
place the spring equilibrium at the origin. Its equation of motion is
thus:
) and will for the time being
place the spring equilibrium at the origin. Its equation of motion is
thus:
| (31) |
Rearranging:
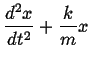 |
(32) | ||
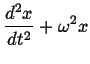 |
(33) |
This latter form is the standard harmonic oscillator equation (of motion). If we solve it once and for all now, whenever we can put an equation of motion into this form in the future we can just read off the solution by identifying similar quantities.
To solve it, we note that it basically tells us that ![]() must be a
function that has a second derivative proportional to the function
itself. We know at least three functions whose second derivatives are
proportional to themselves: cosine, sine and exponential. To learn
something very important about the relationship between these functions,
we'll assume the exponential form:
must be a
function that has a second derivative proportional to the function
itself. We know at least three functions whose second derivatives are
proportional to themselves: cosine, sine and exponential. To learn
something very important about the relationship between these functions,
we'll assume the exponential form:
| (34) |
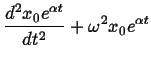 |
(35) | ||
| (36) | |||
| (37) |
Clearly:
| (38) |
| (39) | |||
| (40) |
| (41) |