$\mbox{\boldmath$E$}$ Perpendicular to Plane of Incidence

The electric field in this case is perforce parallel to the surface and hence $\mbox{\boldmath$E$}\cdot\hat{\mbox{\boldmath$n$}} = 0$ and $\vert\mbox{\boldmath$E$}\times\hat{\mbox{\boldmath$n$}}\vert = 1$ (for incident, reflected and refracted waves). Only two of the four equations above are thus useful. The $\mbox{\boldmath$E$}$ equation is trivial. The $\mbox{\boldmath$B$}$ equation requires us to determine the magnitude of the cross product of $\mbox{\boldmath$B$}$ of each wave with $\hat{\mbox{\boldmath$n$}}$. 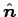Let's do one component as an example. 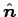Examining the triangle formed between $\mbox{\boldmath$B$}_0$ and $\hat{\mbox{\boldmath$n$}}$ for the incident waves (where $\theta_i$ is the angle of incidence and/or reflection, and $\theta_r$ is the angle of refraction), we see that:

$$\frac{1}{\mu}\vert\mbox{\boldmath$B$}_0 \times \hat{\mbox{\boldmath$n$}}\vert = \frac{1}{\mu} B_0 \cos(\theta_i)$$

$$= \frac{\sqrt{\mu \epsilon}}{\mu} E_0 \cos(\theta_i)$$

$$= \sqrt{\frac{\epsilon}{\mu}} E_0 \cos(\theta_i)$$ (9.61)

Repeating this for the other two waves and collecting the results, we obtain:

$$E_0 + E_0'' = E_0'$$ (9.62)

$$\sqrt{\frac{\epsilon}{\mu}} (E_0 - E_0'')\cos(\theta_i) = \sqrt{\frac{\epsilon'}{\mu'}} E_0'\cos(\theta_r)$$ (9.63)

This is two equations with two unknowns. Solving it is a bit tedious. We need:

$$\cos(\theta_r) = \sqrt{1 - \sin^2(\theta_r)}$$ (9.64)

$$= \sqrt{1 - \frac{n^2}{n'^2}\sin^2(\theta_i)}$$ (9.65)

$$= \frac{\sqrt{n'^2 - n^2\sin^2(\theta_i)}}{n'}$$ (9.66)

Then we (say) eliminate $E_0'$ using the first equation:

$$\sqrt{\frac{\epsilon}{\mu}} (E_0 - E_0'')\cos(\theta_i) = \... ...} (E_0 + E_0'') \frac{\sqrt{n'^2 - n^2\sin^2(\theta_i)}}{n'}$$ (9.67)

Collect all the terms:

$$E_0 \left( \sqrt{\frac{\epsilon}{\mu}} \cos(\theta_i) - \sqrt{\fr... ...n'}{\mu'}} \frac{\sqrt{n'^2 - n^2\sin^2(\theta_i)}}{n'} \right) = \hspace*{2cm}$$

$$E_0''\left(\sqrt{\frac{\epsilon'}{\mu'}}\frac{\sqrt{n'^2 - n^2\sin^2(\theta_i)}}{n'} + \sqrt{\frac{\epsilon}{\mu}} \cos(\theta_i) \right)$$ (9.68)

Solve for $E_0''$:

$$E_0'' = E_0 \frac{ \left( \sqrt{ \frac{\epsilon}{\mu} } \... ...\frac{ \sqrt{n'^2 - n^2\sin^2(\theta_i)} }{ n' } \right) }$$ (9.69)

This expression can be simplified after some tedious cancellations involving

$$\frac{n}{n'} = \sqrt{\frac{\mu \epsilon}{\mu'\epsilon'}}$$ (9.70)

and either repeating the process or back-substituting to obtain :

$$E_0'' = E_0 \frac{ \left( n\cos(\theta_i) - \frac{\mu}{\mu'}\sqrt{ n'^2 -... ... n\cos(\theta_i) + \frac{\mu}{\mu'}\sqrt{n'^2 - n^2\sin^2(\theta_i) } \right) }$$ (9.71)

$$E_0' = E_0 \frac{ 2n\cos(\theta_i) }{ \left( n\cos(\theta_i) + \frac{\mu}{\mu'}\sqrt{n'^2 - n^2\sin^2(\theta_i) } \right) }$$ (9.72)