Table of Properties of Vector Harmonics

Basic Definitions

$\displaystyle \mbox{\boldmath$Y$}_{\ell \ell}^{m}$	$\textstyle =$	$\displaystyle \frac{1}{\sqrt{\ell(\ell+1)}} \mbox{\boldmath$L$}Y_{\ell,m}$
$\displaystyle \mbox{\boldmath$Y$}_{\ell \ell-1}^{m}$	$\textstyle =$	$\displaystyle -\frac{1}{\sqrt{\ell(2\ell+1)}} \left[ -\ell \hat{\mbox{\boldmath$r$}}+ i\hat{\mbox{\boldmath$r$}}\times\mbox{\boldmath$L$}\right]Y_{\ell,m}$
$\displaystyle \mbox{\boldmath$Y$}_{\ell \ell+1}^{m}$	$\textstyle =$	$\displaystyle -\frac{1}{\sqrt{(\ell+1)(2\ell+1)}} \left[ (\ell+1) \hat{\mbox{\boldmath$r$}}+ i\hat{\mbox{\boldmath$r$}}\times\mbox{\boldmath$L$}\right]Y_{\ell,m}$

Eigenvalues ( $j,\ell,m$ are integral):

$\displaystyle J^2 \mbox{\boldmath$Y$}_{j \ell}^{m}$	$\textstyle =$	$\displaystyle j(j+1)\mbox{\boldmath$Y$}_{j \ell}^{m}$
$\displaystyle L^2 \mbox{\boldmath$Y$}_{j \ell}^{m}$	$\textstyle =$	$\displaystyle \ell(\ell+1)\mbox{\boldmath$Y$}_{j \ell}^{m}$
$\displaystyle J_z \mbox{\boldmath$Y$}_{j \ell}^{m}$	$\textstyle =$	$\displaystyle m \mbox{\boldmath$Y$}_{j \ell}^{m}$

Projective Orthonormality:

$\begin{displaymath} \int \mbox{\boldmath$Y$}_{j \ell}^{m}\cdot\mbox{\boldmath$Y$... ...d\Omega = \delta_{jj'}\delta_{\ell\ell'}\delta_{mm'} \nonumber \end{displaymath}$

Complex Conjugation:

$\begin{displaymath} \mbox{\boldmath$Y$}_{j \ell}^{m \ast} = (-1)^{\ell + 1 - j} (-1)^m \mbox{\boldmath$Y$}_{j \ell}^{-m} \end{displaymath}$

Addition Theorem (LCB notes corrupt - this needs to be checked):

$\displaystyle \mbox{\boldmath$Y$}_{j \ell}^{m \ast}\cdot\mbox{\boldmath$Y$}_{j' \ell'}^{m'}$	$\textstyle =$	$\displaystyle \sum_n (-1)^{m+1}\sqrt{\frac{(2\ell+1)(2\ell'+1)(2j'+1)(2j+1)}{4\pi (2n+1)}} \times$
		$\displaystyle \quad\quad C_{000}^{\ell\ell'n}C_{0,-m,m'}^{jj'n} W(j\ell j'\ell';n) Y_{n,(m'-m)}$

For

any function of

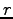only:

$\displaystyle \mbox{\boldmath$\nabla$}\cdot (\mbox{\boldmath$Y$}_{\ell \ell}^{m}F)$	$\textstyle =$	$\displaystyle 0$
$\displaystyle \mbox{\boldmath$\nabla$}\cdot (\mbox{\boldmath$Y$}_{\ell \ell-1}^{m}F)$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell}{2\ell+1}} \left[ (\ell-1)\frac{F}{r} - \frac{dF}{dr}\right] Y_{\ell,m}$
$\displaystyle \mbox{\boldmath$\nabla$}\cdot (\mbox{\boldmath$Y$}_{\ell \ell+1}^{m}F)$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell+1}{2\ell+1}} \left[ (\ell+2)\frac{F}{r} - \frac{dF}{dr}\right] Y_{\ell,m}$

Ditto:

$\displaystyle i\mbox{\boldmath$\nabla$}\times (\mbox{\boldmath$Y$}_{\ell \ell}^{m}F)$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell+1}{2\ell+1}} \left[ (\ell+1)\frac{F}{r} + \frac{... ...ft[-\ell\frac{F}{r} + \frac{dF}{dr}\right]\mbox{\boldmath$Y$}_{\ell \ell+1}^{m}$
$\displaystyle i\mbox{\boldmath$\nabla$}\times (\mbox{\boldmath$Y$}_{\ell \ell-1}^{m}F)$	$\textstyle =$	$\displaystyle -\sqrt{\frac{\ell+1}{2\ell+1}} \left[ (\ell-1)\frac{F}{r} - \frac{dF}{dr}\right]\mbox{\boldmath$Y$}_{\ell \ell}^{m}$
$\displaystyle i\mbox{\boldmath$\nabla$}\times (\mbox{\boldmath$Y$}_{\ell \ell+1}^{m}F)$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell}{2\ell+1}} \left[ (\ell+2)\frac{F}{r} - \frac{dF}{dr}\right]\mbox{\boldmath$Y$}_{\ell \ell}^{m}$

This puts the VSHs into vector form:

$\begin{displaymath} \mbox{\boldmath$Y$}_{\ell \ell}^{m} = \left( \begin{array}{c... ...\ell+m+1)}{2\ell(\ell+1)}} Y_{\ell,m+1} \\ \end{array}\right) \end{displaymath}$

$\begin{displaymath} \mbox{\boldmath$Y$}_{\ell \ell-1}^{m} = \left( \begin{array}... ...ell-m)}{2\ell(2\ell-1)}} Y_{\ell-1,m+1} \\ \end{array}\right) \end{displaymath}$

$\begin{displaymath} \mbox{\boldmath$Y$}_{\ell \ell+1}^{m} = \left( \begin{array}... ...1)}{2(\ell+1)(2\ell+3)}} Y_{\ell+1,m+1} \\ \end{array}\right) \end{displaymath}$

Hansen Multipole Properties

$\displaystyle \mbox{\boldmath$\nabla$}\cdot {\mbox{\boldmath$M$}_L}$	$\textstyle =$	$\displaystyle 0$
$\displaystyle \mbox{\boldmath$\nabla$}\cdot {\mbox{\boldmath$N$}_L}$	$\textstyle =$	$\displaystyle 0$
$\displaystyle \mbox{\boldmath$\nabla$}\cdot {\mbox{\boldmath$L$}_L}$	$\textstyle =$	$\displaystyle i k f_\ell(kr) Y_L(\hat{\mbox{\boldmath$r$}})$

$\displaystyle \mbox{\boldmath$\nabla$}\times {\mbox{\boldmath$M$}_L}$	$\textstyle =$	$\displaystyle -ik \mbox{\boldmath$N$}_L$
$\displaystyle \mbox{\boldmath$\nabla$}\times {\mbox{\boldmath$N$}_L}$	$\textstyle =$	$\displaystyle ik \mbox{\boldmath$M$}_L$
$\displaystyle \mbox{\boldmath$\nabla$}\times {\mbox{\boldmath$L$}_L}$	$\textstyle =$	$\displaystyle 0$

Hansen Multipole Explicit Forms

$\displaystyle \mbox{\boldmath$M$}_L$	$\textstyle =$	$\displaystyle f_\ell(kr) \mbox{\boldmath$Y$}_{\ell \ell}^{m}$
$\displaystyle \mbox{\boldmath$N$}_L$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell+1}{2 \ell +1}} f_{\ell - 1}(kr) \mbox{\boldmath$... ...\frac{\ell}{2 \ell + 1}} f_{\ell + 1}(kr) \mbox{\boldmath$Y$}_{\ell,\ell+1}^{m}$
$\displaystyle \mbox{\boldmath$L$}_L$	$\textstyle =$	$\displaystyle \sqrt{\frac{\ell}{2 \ell + 1}} f_{\ell - 1}(kr) \mbox{\boldmath$Y... ...frac{\ell+1}{2 \ell +1}} f_{\ell + 1}(kr) \mbox{\boldmath$Y$}_{\ell,\ell+1}^{m}$

$\displaystyle \mbox{\boldmath$M$}_L$	$\textstyle =$	$\displaystyle f_\ell(kr) \mbox{\boldmath$Y$}_{\ell \ell}^{m}$
$\displaystyle \mbox{\boldmath$N$}_L$	$\textstyle =$	$\displaystyle \frac{1}{kr} \bigg\{ \frac{d }{d(kr)} (kr f_\ell) \big(i\hat{\m... ...}^{m} \big) - \hat{\mbox{\boldmath$r$}}\sqrt{\ell(\ell + 1)} f_\ell Y_L \bigg\}$
$\displaystyle \mbox{\boldmath$L$}_L$	$\textstyle =$	$\displaystyle \sqrt{\ell(\ell + 1)} \frac{1}{kr} (i \hat{\mbox{\boldmath$r$}} \... ...ell}^{m}) - \hat{\mbox{\boldmath$r$}}\bigg[\frac{d }{d(kr)} f_\ell \bigg] Y_L$