| (86) |
The slope of a line is defined to be the rise divided by the run. For a curved line, however, the slope has to be defined at a point. Lines (curved or straight, but not infinitely steep) can always be thought of as functions of a single variable. We call the slope of a line evaluated at any given point its derivative, and call the process of finding that slope taking the derivative of the function.
Later we'll say a few words about multivariate (vector) differential calculus, but that is mostly beyond the scope of this course.
The definition of the derivative of a function is:
| (86) |
First, note that:
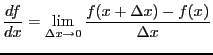 |
(87) |
Second, differentiation is linear. That is:
 |
(88) |
Third, suppose that  (the product of two functions). Then
(the product of two functions). Then
 |
|||
 |
|||
 |
(89) |
 we obtain the following rule for the
differential of a product:
we obtain the following rule for the
differential of a product:
| (90) |
We can easily and directly compute the derivative of a mononomial:
 |
|||
| (91) |
 |
|||
 |
|||
| (92) |
Again it is beyond the scope of this short review to completely
rederive all of the results of a calculus class, but from what has been
presented already one can see how one can systematically proceed. We
conclude, therefore, with a simple table of useful derivatives and
results in summary (including those above):
| (93) | |||
 |
(94) | ||
| (95) | |||
 |
 |
(96) | |
 |
(97) | ||
 |
(98) | ||
 |
 |
(99) | |
 |
(100) | ||
| (101) | |||
 |
(102) | ||
 |
(103) | ||
 |
(104) | ||
 |
(105) | ||
 |
(106) |