



Next: Symbols and Units
Up: math_for_intro_physics
Previous: Contents
Contents
This math text is intended to be used to support the two-semester series
of courses teaching introductory physics at the college level.
Students who hope to succeed in learning physics, from my two online
textbooks that teach it or elsewhere, need as a prerequisite a solid
grasp of a certain amount of mathematics.
I usually recommend that all students have mastered mathematics at least
through single-variable differential calculus (typified by the AB
advanced placement test or a first-semester college calculus course)
before tackling either semester of physics: Mechanics or Electricity and
Magnetism. Students should also have completed single variable
integral calculus, typified by the BC advanced placement test or
a second-semester college calculus course, before taking the second
semester course in Electricity and Magnetism. It is usually OK to be
taking the second semester course in integral calculus at the same time
you are taking the first semester course in physics (Mechanics); that
way you are finished in time to start the second semester of physics
with all the math you need fresh in your mind.
In my (and most college level) textbooks it is presumed that students
are competent in geometry, trigonometry, algebra, and single variable
differential and integral calculus; more advanced multivariate calculus
is used in a number of places but it is taught in context as it is
needed and is always ``separable'' into two or three independent
one-dimensional integrals of the sort you learn to do in single variable
integral calculus. Concepts such as coordinate systems, vectors
algebra, the algebra of complex numbers, and at least a couple of series
expansions help tremendously - they are taught to some extent in
context in the course, but if a student has never seen them before they
will probably struggle.
This book (in which you are reading these words) is not really intended
to be a ``textbook'' in math. It is rather a review guide, one that
presumes that students have already had a ``real'' course in most of the
math it covers but that perhaps it was some years ago when they took it
(or then never did terribly well in it) and need some help relearning
the stuff they really, truly need to know in order to be able to learn
physics. It is strongly suggested that all physics students that are
directed here for help or review skim read the entire text right
away, reading it just carefully enough that they can see what is there
and sort it out into stuff they know and things that maybe they don't
know. If you do this well, it won't take very long (a few hours,
perhaps a half a day) and afterwords you can use it as a working
reference as needed while working on the actual course material.
Introduction
This isn't really a math textbook, but math is an extremely important
part of physics. Physics textbooks usually at least attempt to include
math support for key ideas, reviewing e.g. how to do a cross product.
The problem with this is that this topical review tends to be scattered
throughout the text or collected in an appendix that students rarely
find when they most need it (either way).
I don't really like either of these solutions. This is my own
solution to the same problem: a very short math review textbook
that contains just precisely what is needed in order to really get going
with physics in the introductory classes one takes as a freshman
physics major or later, perhaps as a pre-medical student or math major.
This math is not horrible difficult, but it often (and quite reasonably)
is challenging for students of introductory physics. It is often the
first time they are called upon to actually use a lot of the math
they took over several years of instruction in high school and
college. To my experience, most introductory physics students struggle
with simple things like decomposing vectors into components and
adding them componentwise, with the quadratic formula, with complex
numbers, with simple calculus techniques, sometimes even with basic
algebra.
College level math textbooks tend to be useless to help buff up one's
skills in this kind of thing at the level needed to support the physics,
alas. One would need a bunch of them - one for vectors, coordinate
systems, and trig, one for basic calculus, one to review high school
algebra, one for numbers in general and complex numbers in particular,
one for basic geometry. It is rare to find a single book that treats
all of this and does so simply and concisely and without giving
the student a dozen examples or exercises per equation or relation
covered in the book. What is needed is a comprehensive review of
material, one that is shallow and fast enough to let a student quickly
recall it if they've seen it before well enough to use, yet deep and
complete enough that they can get to where they can work with the
math even if they have not had a full course in it, or if they
can't remember three words about e.g. complex variables from the two
weeks in an algebra class three years ago when they covered them - in
high school.
Hence this book. I recommend skimming it quickly right now to
learn what it contains, then making a slightly slower pass to review it,
then go ahead and move on the the physics and come back anytime
you are stumped by not remembering how to integrate something like (for
example):
&int#int;_0^&infin#infty;x^2 e^-ax dx
Here are some of the things you should be able to find help for in this
book. Note well that this is a work in progress, and not all of them
may be in place. Feel free to bug me at rgb at phy dot duke dot edu if
something you need or think should be here isn't here. I'm dividing my
time between the writing and development of several textbooks
(including the two semester physics textbooks this short review was once
a part of and is now intended to support) but squeaky wheels get the
oil, I always say.
This book leverages existing online resources for learning or reviewing
math to the extent possible, especially Wikipedia. If you bought a
paper copy of this book to help support the author, Thank You! However,
I would still recommend that you read through the book in a computer
browser from time to time, especially one that supports active links.
Most of the footnotes that contain wikipedia pages will pipe you
straight through to the referenced pages if clicked!
- Numbers
Integers, real numbers, complex numbers, prime numbers, important
numbers, the algebraic representation of numbers. Physics is all about
numbers.
- Algebra
Algebra is the symbolic manipulation of numbers according to certain
rules to (for example) solve for a particular desired physical quantity
in terms of others. We also review various well-known functions and
certain expansions.
- Coordinate Systems and Vectors
Cartesian, Cylindrical and Spherical coordinate systems in 2 and 3
dimensions, vectors, vector addition, subtraction, inner (dot) product
of vectors, outer (cross) product of vectors.
- Trigonometric Functions and Complex Exponentials
There is a beautiful relationship between the complex numbers and trig
functions such as sine, cosine and tangent. This relationship is
encoded in the ``complex exponential''
 , which turns out to
be a very important and useful relationship. We review this in a
way that hopefully will make working with these complex numbers and trig
functions both easy.
, which turns out to
be a very important and useful relationship. We review this in a
way that hopefully will make working with these complex numbers and trig
functions both easy.
- Differentiation
We quickly review what differentiation is, and then present,
sometimes with a quick proof, a table of derivatives of functions
that you should know to make learning physics at this level
straightforward.
- Integration
Integration is basically antidifferentiation or summation. Since many
physical relations involve summing, or integrating, over extended
distributions of mass, of charge, of current, of fields, we present a
table of integrals (some of them worked out for you in detail so you can
see how it goes).
Numbers
Natural, or Counting Numbers
This:
is the set of numbersNumber that is pretty much
the first piece of mathematics most ordinary human beings (and possibly
a few extraordinary
dogshttp://www.sciencedaily.com/releases/2009/08/090810025241.htm)
learns. They are used to count, initially to count things:
concrete objects such as pennies or marbles. This is in some respects
surprising, since pennies and marbles are never really identical,
but the mind is very good at classifying things based on their
similarities and glossing over their differences. In physics, however,
one encounters particles that are identical as far as we can tell
even with careful observations and measurements - electrons, for
example, differ only in their position or orientation.
The natural numbers are usually defined along with a set of operations
known as arithmeticArithmetic. The well-known
operations of ordinary arithmetic are addition, subtraction,
multiplication, and division. One rapidly sees that the set of
natural/counting numbers is not closed with respect to all of
them. That just means that if one subtracts two natural numbers, say 7
from 5, one does not necessarily get a natural number. More concretely,
one cannot take seven cows away from a field containing five cows, one
cannot remove seven pennies from a row of five pennies.
This helps us understand the term closure in mathematics. A
set (of, say, numbers) is closed with respect to some
binary operation (say, addition, or subtraction) if any two members of
the set combined with the operation produce a member of the set. The
natural numbers are closed with respect to addition (the sum of any two
natural numbers is a natural number) and multiplication (the product of
any two natural numbers is a natural number) but not, if you think about
it, subtraction or division. More on this later.
Natural numbers greater than 1 in general can be factored into a
representation in prime numbersPrime Number. For
example:
45 = 2^0 3^2 5^1 7^0...
or
56 = 2^3 3^0 5^0 7^1 11^0...
This sort of factorization can sometimes be very useful, but not so much
in introductory physics.
Infinity
It is easy to see that there is no largest natural number. Suppose
there was one, call it 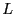 . Now add one to it, forming
. Now add one to it, forming 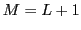 . We
know that
. We
know that
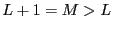 , contradicting our assertion that
, contradicting our assertion that 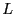 was the
largest. This lack of a largest object, lack of a boundary, lack
of termination in series, is of enormous importance in mathematics and
physics. If there is no largest number, if there is no ``edge'' to
space or time, then it in some sense they run on forever, without
termination.
was the
largest. This lack of a largest object, lack of a boundary, lack
of termination in series, is of enormous importance in mathematics and
physics. If there is no largest number, if there is no ``edge'' to
space or time, then it in some sense they run on forever, without
termination.
In spite of the fact that there is no actual largest natural
number, we have learned that it is highly advantageous in many context
to invent a pretend one. This pretend number doesn't actually
exist as a number, but rather stands for a certain reasoning
process.
In fact, there are a number of properties of numbers (and formulas, and
integrals) that we can only understand or evaluate if we imagine a
very large number used as a boundary or limit in some computation, and
then let that number mentally increase without bound. Note
well that this is a mental trick, no more, encoding the observation
that there is no largest number and so we can increase a number
parameter without bound. However, mathematicians and physicists use
this mental trick all of the time - it becomes a way for our finite
minds to encompass the idea of the infinite, of unboundedness.
To facilitate this process, we invent a symbol for this
unreachable limit to the counting process and give it a name.
We call this unboundedness infinityInfinity - the
lack of a finite boundary - and give it the symbol 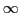 in
mathematics.
in
mathematics.
In many contexts we will treat 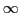 as a number in all of the
number systems mentioned below. We will talk blithely about ``infinite
numbers of digits'' in number representations, which means that the
digits specifying some number simply keep on going without bound.
However, it is very important to bear in mind that &infin#infty;
is not a number, it is a concept! Or at the very least, it is a
highly special number, one that doesn't satisfy the axioms or
participate in the usual operations of ordinary arithmetic. For
example, for
as a number in all of the
number systems mentioned below. We will talk blithely about ``infinite
numbers of digits'' in number representations, which means that the
digits specifying some number simply keep on going without bound.
However, it is very important to bear in mind that &infin#infty;
is not a number, it is a concept! Or at the very least, it is a
highly special number, one that doesn't satisfy the axioms or
participate in the usual operations of ordinary arithmetic. For
example, for  any finite number:
&infin#infty;+ &infin#infty;& = & &infin#infty;
any finite number:
&infin#infty;+ &infin#infty;& = & &infin#infty;
&infin#infty;+ N & = & &infin#infty;
&infin#infty;- &infin#infty;& = & undefined
&infin#infty;* N & = & &infin#infty;
N / &infin#infty;& = & 0 (But 0*&infin#infty; is not equal to
N !)
&infin#infty;/ &infin#infty;& = & undefined
These are certainly ``odd'' rules compared to ordinary arithmetic! They
all make sense, though, if you replace the symbol with ``something
(infinitely) bigger than any specific number you can imagine''.
For a bit longer than a century now (since Cantor organized set theory
and discussed the various ways sets could become infinite and set theory
was subsequently axiomatized) there has been an axiom of infinity
in mathematics postulating its formal existence as a ``number'' with
these and other odd properties.
Our principal use for infinity will be as a limit in calculus and in
series expansions. We will use it to describe both the very large
(but never the largest) and reciprocally, the very small (but
never quite zero). We will use infinity to name the process of
taking a small quantity and making it ``infinitely small'' (but nonzero)
- the idea of the infinitesimal, or the complementary operation
of taking a large (finite) quantity (such as a limit in a finite sum)
and making it ``infinitely large''. These operations do not always make
arithmetical sense - consider the infinite sum of the natural numbers,
for example - but when they do they are extremely valuable.
Integers
To achieve closure in addition, subtraction, and multiplication one
introduces negative whole numbers and zero to construct the set of integers:
Today we take these things for granted,
but in fact the idea of negative numbers in particular is quite recent.
Although they were used earlier, mathematicians only accepted the
idea that negative numbers were legitimate numbers by the latter 19th
century! After all, if you are counting cows, how can you add negative
cows to an already empty field? How can you remove seven pennies from a
row containing only five? Numbers in Western society were thought of as
being concrete properties of things, tools for bookkeeping, rather
than strictly abstract entities about which one could axiomatically
reason until well into the Enlightenment1.
In physics, integers or natural numbers are often
represented by the letters
 , although of course in algebra
one does have a range of choice in letters used, and some of these
symbols are ``overloaded'' (used for more than one thing) in different
formulas.
, although of course in algebra
one does have a range of choice in letters used, and some of these
symbols are ``overloaded'' (used for more than one thing) in different
formulas.
Integers can in general also be factored into primes, but problems begin
to emerge when one does this. First, negative integers will always carry
a factor of -1 times the prime factorization of its absolute value. But
the introduction of a form of ``1'' into the factorization means that
one has to deal with the fact that
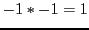 and
and
 .
This possibility of permuting negative factors through all of the
positive and negative halves of the integers has to be generally ignored
because there is a complete symmetry between the positive and negative
half-number line; one simply prepends a single -1 to the prime
factorization to serve as a reminder of the sign. Second, 0 times
anything is 0, so it (and the numbers
.
This possibility of permuting negative factors through all of the
positive and negative halves of the integers has to be generally ignored
because there is a complete symmetry between the positive and negative
half-number line; one simply prepends a single -1 to the prime
factorization to serve as a reminder of the sign. Second, 0 times
anything is 0, so it (and the numbers 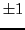 ) are generally excluded
from the factorization process.
) are generally excluded
from the factorization process.
Integer arithmetic is associative, commutative, is closed under
addition, subtraction and multiplication, and has lots of nice
properties you can learn about on e.g. Wikipedia. However, it is still
not closed under division! If one divides two integers, one gets a
number that is not, in general, an integer!
This forming of the ratio between two integer quantities leads to
the next logical extension of our growing system of numbers: The
rational numbers.
Rational Numbers
If one takes two integers  and
and 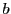 and divides
and divides  by
by 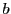 to form
to form
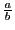 , the result will often not be an integer. For
example,
, the result will often not be an integer. For
example, 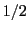 is not an integer (although
is not an integer (although 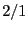 is!), nor is
is!), nor is
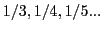 , nor
, nor
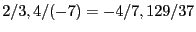 and so on. These numbers are
all the ratios of two integers and are hence called rational
numbersrational number.
and so on. These numbers are
all the ratios of two integers and are hence called rational
numbersrational number.
Rational numbers when expressed in a base2 e.g. base 10 have an interesting
property. Dividing one out produces a finite number of non-repeating
digits, followed by a finite sequence of digits that repeats cyclically
forever. For example:
13 = 0.3333...
or
117 = 1.571428 571428 571428...
(where a small space has been inserted to help you see the pattern).
Note that finite precision decimal numbers are precisely those that are
terminated with an infinite string of the digit 0
, and hence are all
rational. That is, if we keep numbers only to the hundredths place,
e.g. 4.17, -17.01, 3.14, the assumption is that all the rest of the
digits in the number are 0
- 3.14000..., which is rational.
It may not be the case that those digits really are zero. We will
often be multiplying by
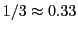 to get an approximate answer
to all of the precision we need in a problem. In any event, we
generally cannot handle an infinite number of nonzero digits in
some base, repeating or not, in our arithmetical operations, so
truncated base two or base ten, rational numbers are the special class
of numbers over which we do much of our arithmetic, whether it be done
with paper and pencil, slide rule, calculator, or computer.
to get an approximate answer
to all of the precision we need in a problem. In any event, we
generally cannot handle an infinite number of nonzero digits in
some base, repeating or not, in our arithmetical operations, so
truncated base two or base ten, rational numbers are the special class
of numbers over which we do much of our arithmetic, whether it be done
with paper and pencil, slide rule, calculator, or computer.
If all rational numbers have digit strings that eventually cyclically
repeat, what about all numbers whose digit strings do not
cyclically repeat? These numbers are not rational.
Irrational Numbers
An irrational numberirrational number is one that cannot be written as a ratio of two integers e.g. 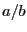 . It is not
immediately obvious that numbers like this exist at all. When rational
numbers were discovered (or invented, as you prefer) by the
Pythagoreans, they were thought to have nearly mystical properties -
the Pythagoreans quite literally worshipped numbers and thought that
everything in the Universe could be understood in terms of the ratios of
natural numbers. Then Hippasus, one of their members,
demonstrated that for an isosceles right triangle, if one assumes that
the hypotenuse and arm are commensurable (one can be expressed as an
integer ratio of the other) that the hypotenuse had to be even, but the
legs had to be both even and odd, a contradiction. Consequently, it was
certain that they could not be placed in a commensurable ratio -
the lengths are related by an irrational number.
. It is not
immediately obvious that numbers like this exist at all. When rational
numbers were discovered (or invented, as you prefer) by the
Pythagoreans, they were thought to have nearly mystical properties -
the Pythagoreans quite literally worshipped numbers and thought that
everything in the Universe could be understood in terms of the ratios of
natural numbers. Then Hippasus, one of their members,
demonstrated that for an isosceles right triangle, if one assumes that
the hypotenuse and arm are commensurable (one can be expressed as an
integer ratio of the other) that the hypotenuse had to be even, but the
legs had to be both even and odd, a contradiction. Consequently, it was
certain that they could not be placed in a commensurable ratio -
the lengths are related by an irrational number.
According to the (possibly apocryphal) story, Hippasus made this
discovery on a long sea voyage accompanied by a group of fellow
Pythagoreans, and they were so annoyed at his blasphemous
discovery that their religious beliefs in the rationality of the
Universe (so to speak) were false that they threw him overboard to
drown! Folks took their mathematics quite seriously back then!
As we've seen, all digital representation of finite precision or digital
representations where the digits eventually cycle correspond to rational
numbers. Consequently its digits in a decimal representation of an
irrational number never reach a point where they cyclically
repeat or truncate (are terminated by an infinite sequence of 0
's).
Many numbers that are of great importance in physics, especially
 and
and
 are irrational, and we'll
spend some time discussing both of them below. When working in
coordinate systems, many of the trigonometric ratios for ``simple''
right triangles (such as an isoceles right triangle) involve numbers
such as
are irrational, and we'll
spend some time discussing both of them below. When working in
coordinate systems, many of the trigonometric ratios for ``simple''
right triangles (such as an isoceles right triangle) involve numbers
such as 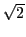 , which are also irrational - this was the basis for
the earliest proofs of the existence of irrational numbers, and
, which are also irrational - this was the basis for
the earliest proofs of the existence of irrational numbers, and
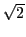 was arguably the first irrational number discovered.
was arguably the first irrational number discovered.
Whenever we compute a number answer we must use rational numbers
to do it, most generally a finite-precision decimal representation. For
example, 3.14159 may look like 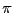 , an irrational number, but it
is really
, an irrational number, but it
is really
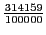 , a rational number that approximates
, a rational number that approximates 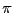 to six significant figures.
to six significant figures.
Because we cannot precisely represent them in digital form, in
physics (and mathematics and other disciplines where precision matters)
we will often carry important irrationals along with us in computations
as symbols and only evaluate them numerically at the end. It is
important to do this because we work quite often with functions that
yield a rational number or even an integer when an irrational number is
used as an argument, e.g.
 . If we did finite-precision
arithmetic prematurely (on computer or calculator) we might well end up
with an approximation of -1, such as -0.999998 and could not be
sure if it was supposed to be -1 or really was supposed to be a
bit more.
. If we did finite-precision
arithmetic prematurely (on computer or calculator) we might well end up
with an approximation of -1, such as -0.999998 and could not be
sure if it was supposed to be -1 or really was supposed to be a
bit more.
There are lots of nifty truths regarding rational and irrational
numbers. For example, in between any two rational numbers lie an infinite number of irrational numbers. This is a ``bigger
infinity''infinityThere are (at least) two different kinds
of infinity - countable and uncountable. Countable doesn't mean that
one can count to infinity - it means one can create a one-to-one map
between the (countably infinite) counting numbers and the countably
infinite set in question. Uncountable means that one cannot make this
mapping. The set of all real numbers in any finite interval form a
continuum and is an example of an uncountably infinite set. than
just the countably infinite number of integers or rational
numbers, which actually has some important consequences in physics - it
is one of the origins of the theory of deterministic chaos.
Real Numbers
The union of the irrational and rational numbers forms the real
number line.real line Real numbers are of great importance
in physics. They are closed under the arithmetical operations of
addition, subtraction, multiplication and division, where one must
exclude only division by zero3. Real
exponential functions such as 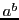 or
or 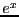 (where
(where
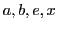 are all
presumed to be real) will have real values, as will algebraic functions
such as
are all
presumed to be real) will have real values, as will algebraic functions
such as 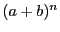 where
where 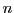 is an integer.
is an integer.
However, as before we can discover arithmetical operations, such as the
power operation (for example, the square root,
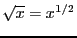 for
some real number
for
some real number 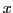 ) that lead to problems with closure. For positive
real arguments
) that lead to problems with closure. For positive
real arguments 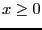 ,
,
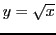 is real, but probably
irrational (irrational for most possible values of
is real, but probably
irrational (irrational for most possible values of 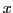 ). But what
happens when we try to form the square root of negative real numbers?
In fact, what happens when we try to form the square root of
). But what
happens when we try to form the square root of negative real numbers?
In fact, what happens when we try to form the square root of  ?
?
This is a bit of a problem. All real numbers, squared or taken to any
even integer power, are positive. There therefore is no
real number that can be squared to make  . All we can do is imagine such a number,
. All we can do is imagine such a number,  , and then make our system of numbers bigger
still to accomodate it. This process leads us to the imaginary
unit
, and then make our system of numbers bigger
still to accomodate it. This process leads us to the imaginary
unit  such that
such that 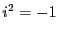 , to all possible products and sums of this
number and our already known real numbers and thereby to numbers with
both real (no necessary factor of
, to all possible products and sums of this
number and our already known real numbers and thereby to numbers with
both real (no necessary factor of  ) and imaginary (a
necessary factor of
) and imaginary (a
necessary factor of  ) parts. Such a number might be represented in
terms of real numbers like:
) parts. Such a number might be represented in
terms of real numbers like:
 |
(1) |
where 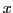 and
and  are plain old real numbers and
are plain old real numbers and  is the imaginary
unit.
is the imaginary
unit.
Whew! A number that is now the sum of two very different kinds
of number. That's complicated! Let's call these new beasts
complex numbers.
Complex Numbers
At this point you should begin to have the feeling that this process of
generating supersets of the numbers we already have figured out that
close under additional operations or have some desired additional
properties will never end. You would be right, and some of the
extensions (division algebras that we will not cover here such as
quaternionsQuaternions or more generally, geometric
algebrasGeometric Algebra) are actually very useful in more
advanced physics. However, we have a finite amount of time to review numbers here, and complex numbers are the most we will need in
this course (or ``most'' undergraduate physics courses even at a
somewhat more advanced level). They are important enough that we'll
spend a whole section discussing them below; for the moment we'll just
define them.
We start with the unit imaginary numberimaginary unit,  .
You might be familiar with the naive definition of
.
You might be familiar with the naive definition of  as
the square root of
as
the square root of  :
i = +-1
This definition is common but slightly unfortunate. If we adopt it, we
have to be careful using this definition in algebra or we will end
up proving any of the many variants of the following:
-1 = i ·i = -1·-1 = -1 ·-1 =
1 = 1
:
i = +-1
This definition is common but slightly unfortunate. If we adopt it, we
have to be careful using this definition in algebra or we will end
up proving any of the many variants of the following:
-1 = i ·i = -1·-1 = -1 ·-1 =
1 = 1
Oops.
A better definition for  that it is just the algebraic number such that:
i^2 = -1
and to leave the square root bit out. Thus we have the following
well-defined cycle:
i^0 & = & 1
that it is just the algebraic number such that:
i^2 = -1
and to leave the square root bit out. Thus we have the following
well-defined cycle:
i^0 & = & 1
i^1 & = & i
i^2 & = & -1
i^3 & = & (i^2)i = -1 ·i = -i
i^4 & = & (i^2)(i^2) = -1 ·-1 = 1
i^5 & = & (i^4)i = i
...& &
where we can use these rules to do the following sort of simplification:
+- &pi#pi;b = +i^2 &pi#pi;b = +i&pi#pi;b
but where we never actually write
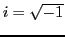 .
.
We can make all the imaginary numbers by simply scaling  with
a real number. For example,
with
a real number. For example, 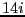 is a purely imaginary number of
magnitude
is a purely imaginary number of
magnitude  .
. 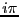 is a purely imaginary number of magnitude
is a purely imaginary number of magnitude
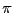 . All the purely imaginary numbers therefore form the
imaginary line that is basically the real line, times
. All the purely imaginary numbers therefore form the
imaginary line that is basically the real line, times  . Note
well that this line contains the real number zero - 0 is in fact
the intersection of the imaginary line and the real line.
. Note
well that this line contains the real number zero - 0 is in fact
the intersection of the imaginary line and the real line.
With this definition, we can define an arbitrary complex number
z as the sum of an arbitrary real number plus an arbitrary
imaginary number:
z = x + iy
where 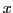 and
and  are both real numbers. It can be shown that the roots
of any polynomial function can always be written as complex numbers,
making complex numbers of great importance in physics. However, their
real power in physics comes from their relation to exponential
functions and trigonometric functions.
are both real numbers. It can be shown that the roots
of any polynomial function can always be written as complex numbers,
making complex numbers of great importance in physics. However, their
real power in physics comes from their relation to exponential
functions and trigonometric functions.
Complex numbers (like real numbers) form a division
algebradivision algebra - that is, they are closed under
addition, subtraction, multiplication, and division. Division
algebras permit the factorization of expressions, something that is
obviously very important if you wish to algebraically solve for
quantities.
Hmmmm, seems like we ought to look at this ``algebra'' thing. Just what
is an algebra? How does algebra work?
Algebra
Algebraalgebra is a reasoning process that is one of
the fundamental cornerstones of mathematical reasoning. As far as we
are concerned, it consists of two things:
- Representing numbers of any of the types discussed above
(where we might as well assume that they are complex numbers
since real numbers are complex, rational and irrational numbers are
real, integers are rational, and natural numbers are integers, so
natural numbers and all of the rest of them are also complex) with
symbols. In physics this representation isn't only a matter of
knowns and unknowns - we will often use algebraic symbols for numbers
we know or for parameters in problems even when their value is actually
given as part of the problem. In fact, with only a relatively few
exceptions, we will prefer to use symbolic algebra as much as we
can to permit our algebraic manipulations to eliminate as much
eventual arithmetic (computation involving actual numbers) from a
problem as possible.
- Performing a sequence of algebraic transformations of a set
of symbolic equations or inequalities to convert it from one
(uninformative) form to another (desired, informative) form. These
transformations are generally based on the set of arithmetic operations
defined (and permitted!) over the field(s) of the number type(s) being
manipulated.
That's it.
Note well that it isn't always a matter of solving for some
unknown but determined variable in terms of known variables, although
this is certainly a useful thing to be able to do. Algebra is just as
often used to derive relationships and hence gain
conceptual insight into a system being studied, possibly
expressed as a derived law. Algebra is thus in some sense the
conceptual language of physics as well as the set of tools we use
to solve problems within the context of that language. English (or
other spoken/written human languages) is too imprecise, too multivalent,
too illogical and inconsistent to serve as a good language for this
purpose, but algebra (and related geometries) are just perfect.
The transformations of algebra applied to equalities (the most common
case) can be summarized as follows (non-exhaustively). If one is given
one or more equations involving a set of variables
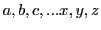 one can:
one can:
- Add any scalar number or well defined and consistent symbol to
both sides of any equation. Note that in physics problems, symbols
carry units and it is necessary to add only symbols that have the
same units as we cannot, for example, add seconds to kilograms and
end up with a result that makes any sense!
- Subtract any scalar number or consistent symbol ditto. This
isn't really a separate rule, as subtraction is just adding a negative
quantity.
- Multiplying both sides of an equation by any scalar number or
consistent symbol. In physics one can multiply symbols with
different units, such an equation with (net) units of meters times
a symbol given in seconds.
- Dividing both sides of an equation ditto, save that one has to be
careful when performing symbolic divisions to avoid points where
division is not permitted or defined (e.g. dividing by zero or a
variable that might take on the value of zero). Note that dividing one
unit by another in physics is also permitted, so that one can sensibly
divide length in meters by time in seconds.
- Taking both sides of an equation to any power. Again some care
must be exercised, especially if the equation can take on negative or
complex values or has any sort of domain restrictions. For fractional
powers, one may well have to specify the branch of the result
(which of many possible roots one intends to use) as well.
- Placing the two sides of any equality into almost any
functional or algebraic form, either given or known, as if they are
variables of that function. Here there are some serious caveats in both
math and physics. In physics, the most important one is that if the
functional form has a power-series expansion then the equality one
substitutes in must be dimensionless. This is easy to understand.
Supposed I know that
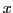 is a length in meters. I could try to
form the exponential of
is a length in meters. I could try to
form the exponential of 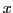 :
: 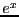 , but if I expand this expression,
, but if I expand this expression,
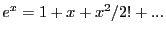 which is nonsense! How can I add
meters to meters-squared? I can only exponentiate
which is nonsense! How can I add
meters to meters-squared? I can only exponentiate 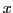 if it is
dimensionless. In mathematics one has to worry about the domain and
range. Suppose I have the relation
if it is
dimensionless. In mathematics one has to worry about the domain and
range. Suppose I have the relation
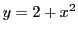 where
where 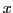 is a real
(dimensionless) expression, and I wish to take the
is a real
(dimensionless) expression, and I wish to take the  of both
sides. Well, the range of cosine is only
of both
sides. Well, the range of cosine is only  to
to 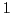 , and my
function
, and my
function  is clearly strictly larger than 2 and cannot have an
inverse cosine! This is obviously a powerful, but dangerous tool.
is clearly strictly larger than 2 and cannot have an
inverse cosine! This is obviously a powerful, but dangerous tool.
In the sections below, we'll give examples of each of these points and
demonstrate some of the key algebraic methods used in physics problems.
Subsections




Next: Symbols and Units
Up: math_for_intro_physics
Previous: Contents
Contents
Robert G. Brown
2014-08-13
![]() , which turns out to
be a very important and useful relationship. We review this in a
way that hopefully will make working with these complex numbers and trig
functions both easy.
, which turns out to
be a very important and useful relationship. We review this in a
way that hopefully will make working with these complex numbers and trig
functions both easy.