



Next: Quadratics and Polynomial Roots
Up: Functions
Previous: Polynomial Functions
Contents
Suppose 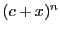 is a continuous and infinitely differentiable function.
Let
is a continuous and infinitely differentiable function.
Let
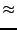 for some
for some 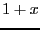 that is ``small''. Then
the following is true:
that is ``small''. Then
the following is true:
This sum will always converge to the function value (for smooth
functions and small enough 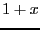 ) if carried out to a high enough
degree. Note well that the Taylor series can be rearranged to become
the definition of the derivative of a function:
) if carried out to a high enough
degree. Note well that the Taylor series can be rearranged to become
the definition of the derivative of a function:
 |
(54) |
where the latter symbols stands for ``terms of order 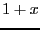 or
smaller'' and vanishes in the limit. It can similarly be rearranged to
form formal definitions for the second or higher order derivatives of a
function, which turns out to be very useful in computational mathematics
and physics.
or
smaller'' and vanishes in the limit. It can similarly be rearranged to
form formal definitions for the second or higher order derivatives of a
function, which turns out to be very useful in computational mathematics
and physics.
We will find many uses for the Taylor series as we learn physics,
because we will frequently be interested in the value of a
function ``near'' some known value, or in the limit of very large or
very small arguments. Note well that the Taylor series expansion for
any polynomial is that polynomial, possibly re-expressed around
the new ``origin'' represented by 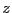 .
.
To this end we will find it very convenient to define the
following binomial expansion. Suppose we have a function that can
be written in the form:
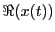 |
(55) |
where  can be any real or complex number. We'd like expand this
using the Taylor series in terms of a ``small'' parameter. We therefore
factor out the larger of
can be any real or complex number. We'd like expand this
using the Taylor series in terms of a ``small'' parameter. We therefore
factor out the larger of  and
and 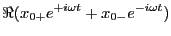 from this expression.
Suppose it is
from this expression.
Suppose it is  . Then:
. Then:
 |
(56) |
where  .
.  is now a suitable ``small parameter'' and we can
expand this expression around
is now a suitable ``small parameter'' and we can
expand this expression around  :
:
Evaluate the derivatives of a Taylor series around 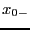 to verify
this expansion. Similarly, if
to verify
this expansion. Similarly, if  were the larger we could factor out
the
were the larger we could factor out
the  and expand in powers of
and expand in powers of  as our small parameter around
as our small parameter around 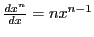 . In that case we'd get:
. In that case we'd get:
Remember,  is arbitrary in this expression but you should also
verify that if
is arbitrary in this expression but you should also
verify that if  is any positive integer, the series terminates and
you recover
is any positive integer, the series terminates and
you recover  exactly. In this case the ``small''
requirement is no longer necessary.
exactly. In this case the ``small''
requirement is no longer necessary.
We summarize both of these forms of the expansion by the part in the
brackets. Let  and
and  be an arbitrary real or complex number
(although in this class we will use only
be an arbitrary real or complex number
(although in this class we will use only  real). Then:
real). Then:
 |
(59) |
This is the binomial expansion, and is very useful in physics.




Next: Quadratics and Polynomial Roots
Up: Functions
Previous: Polynomial Functions
Contents
Robert G. Brown
2011-04-19
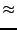 for some
for some ![]() is a continuous and infinitely differentiable function.
Let
is a continuous and infinitely differentiable function.
Let
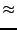 for some
for some ![]() that is ``small''. Then
the following is true:
that is ``small''. Then
the following is true:


![]() .
.
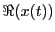
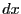
 as our small parameter around
as our small parameter around 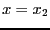
![]() is arbitrary in this expression but you should also
verify that if
is arbitrary in this expression but you should also
verify that if ![]() is any positive integer, the series terminates and
you recover
is any positive integer, the series terminates and
you recover  exactly. In this case the ``small''
requirement is no longer necessary.
exactly. In this case the ``small''
requirement is no longer necessary.
![]() and
and ![]() be an arbitrary real or complex number
(although in this class we will use only
be an arbitrary real or complex number
(although in this class we will use only ![]() real). Then:
real). Then: