| (46) |
A polynomial function is a sum of monomials:
| (46) |
This sum can be finite and terminate at some ![]() (called the degree of the polynomial) or can (for certain series of coefficients
with ``nice'' properties) be infinite and converge to a well defined
function value. Everybody should be familiar with at least the
following forms:
(called the degree of the polynomial) or can (for certain series of coefficients
with ``nice'' properties) be infinite and converge to a well defined
function value. Everybody should be familiar with at least the
following forms:
| (47) | |||
| (48) | |||
| (49) | |||
| (50) |
Polynomial functions are a simple key to a huge amount of mathematics. For example, differential calculus. It is easy to derive:
| (51) |
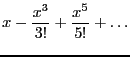 |
(52) |
Next we note that many continuous functions can be defined in terms of their power series expansion. In fact any continuous function can be expanded in the vicinity of a point as a power series, and many of our favorite functions have well known power series that serve as an alternative definition of the function. Although we will not derive it here, one extremely general and powerful way to compute this expansion is via the Taylor series. Let us define the Taylor series and its close friend and companion, the binomial expansion.