 ) associated with its location in space
drawn from the origin to the physical coordinates of the particle
(e.g. - (
) associated with its location in space
drawn from the origin to the physical coordinates of the particle
(e.g. - (
| (16) |
Most motion is not along a straight line. If fact, almost no motion is along a line. We therefore need to be able to describe motion along multiple dimensions (usually 2 or 3). That is, we need to be able to consider and evaluate vector trajectories, velocities, and accelerations. To do this, we must first learn about what vectors are, how to add, subtract or decompose a given vector in its cartesian coordinates (or equivalently how to convert between the cartesian, polar/cylindrical, and spherical coordinate systems), and what scalars are. We will also learn a couple of products that can be constructed from vectors.
A vector in a coordinate system is a directed line between two
points. It has magnitude and direction. Once we define a
coordinate origin, each particle in a system has a position
vector (e.g. -  ) associated with its location in space
drawn from the origin to the physical coordinates of the particle
(e.g. - (
) associated with its location in space
drawn from the origin to the physical coordinates of the particle
(e.g. - (
![]() )):
)):
| (17) |
The position vectors clearly depend on the choice of coordinate origin. However, the difference vector or displacement vector between two position vectors does not depend on the coordinate origin. To see this, let us consider the addition of two vectors:
| (18) |
Note that vector addition proceeds by putting the tail of one at the
head of the other, and constructing the vector that completes the
triangle. To numerically evaluate the sum of two vectors, we
determine their components and add them componentwise, and then
reconstruct the total vector:
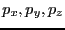 |
(19) | ||
| (20) | |||
| (21) |
If we are given a vector in terms of its length (magnitude)
and orientation (direction angle(s)) then we must evaluate its
cartesian components before we can add them (for example, in 2D):
| (22) | |||
| (23) |
The difference between two vectors is defined by the addition law. Subtraction is just adding the negative of the vector in question, that is, the vector with the same magnitude but the opposite direction. This is consistent with the notion of adding or subtracting its components. Note well: Although the vectors themselves may depend upon coordinate system, the difference between two vectors (also called the displacement if the two vectors are, for example, the postion vectors of some particle evaluated at two different times) does not.
When we reconstruct a vector from its components, we are just using the law of vector addition itself, by scaling some special vectors called unit vectors and then adding them. Unit vectors are (typically perpendicular) vectors that define the essential directions and orientations of a coordinate system and have unit length. Scaling them involves multiplying these unit vectors by a number that represents the magnitude of the vector component. This scaling number has no direction and is called a scalar. Note that the product of a vector and a scalar is always a vector:
| (24) |
 is a vector. In this
case,
is a vector. In this
case,
 is parallel to
is parallel to In addition to multiplying a scalar and a vector together, we can define products that multiply two vectors together. By ``multiply'' we mean that if we double the magnitude of either vector, we double the resulting product - the product is proportional to the magnitude of either vector. There are two such products for the ordinary vectors we use in this course, and both play extremely important roles in physics.
The first product creates a scalar (ordinary number with magnitude but no direction) out of two vectors and is therefore called a scalar product or (because of the multiplication symbol chosen) a dot product. A scalar is often thought of as being a ``length'' (magnitude) on a single line. Multiplying two scalars on that line creates a number that has the units of length squared but is geometrically not an area. By selecting as a direction for that line the direction of the vector itself, we can use the scalar product to define the length of a vector as the square root of the vector magnitude times itself:
| (25) |
From this usage it is clear that a scalar product of two vectors can
never be thought of as an area. If we generalize this idea (preserving
the need for our product to be symmetrically proportional to both
vectors, we obtain the following definition for the general scalar
product:
 |
(26) | ||
| (27) |
This definition can be put into words - a scalar product is the
length of one vector (either one, say ![]() ) times the component of the other vector (
) times the component of the other vector (
![]() ) that points
in the same direction as the vector
) that points
in the same direction as the vector  . Alternatively it
is the length
. Alternatively it
is the length ![]() times the component of
times the component of  parallel to
parallel to
![]() ,
,
![]() . This product is symmetric and commutative (
. This product is symmetric and commutative ( and
and ![]() can appear in
either order or role).
can appear in
either order or role).
The other product multiplies two vectors in a way that creates a third vector. It is called a vector product or (because of the multiplication symbol chosen) a cross product. Because a vector has magnitude and direction, we have to specify the product in such a way that both are defined, which makes the cross product more complicated than the dot product.
As far as magnitude is concerned, we already used the non-areal combination of vectors in the scalar product, so what is left is the product of two vectors that makes an area and not just a ``scalar length squared''. The area of the parallelogram defined by two vectors is just:
| (28) |
 times the
component of
times the
component of  '' or vice versa. Let
us accept this as the magnitude of the cross product (since it clearly
has the proportional property required) and look at the direction.
'' or vice versa. Let
us accept this as the magnitude of the cross product (since it clearly
has the proportional property required) and look at the direction.
The area is nonzero only if the two vectors do not point along the same line. Since two non-colinear vectors always lie in (or define) a plane (in which the area of the parallelogram itself lies), and since we want the resulting product to be independent of the coordinate system used, one sensible direction available for the product is along the line perpendicular to this plane. This still leaves us with two possible directions, though, as the plane has two sides. We have to pick one of the two possibilities by convention so that we can communicate with people far away, who might otherwise use a counterclockwise convention to build screws when we used a clockwise convention to order them, whereupon they send us left handed screws for our right handed holes and everybody gets all irritated and everything.
We therefore define the direction of the cross product using the right hand rule:
Let the fingers of your right hand lie along the direction of the first vector in a cross product (saybelow). Let them curl naturally through the small angle (observe that there are two, one of which is larger than
and one of which is less than
) into the direction of
. The erect thumb of your right hand then points in the general direction of the cross product vector - it at least indicates which of the two perpendicular lines should be used as a direction, unless your thumb and fingers are all double jointed or your bones are missing or you used your left-handed right hand or something.
Putting this all together mathematically, one can show that the following are two equivalent ways to write the cross product of two three dimensional vectors. In components:
| (29) |
| (30) |
Alternatively in many problems it is easier to just use the form:
| (31) |
Note that this axial property of cross products is realized in nature by things that twist or rotate around an axis. A screw advances into wood when twisted clockwise, and comes out of wood when twisted counterclockwise. If you let the fingers of your right hand curl around the screw in the direction of the twist your thumb points in the direction the screw moves, whether it is in or out of the wood. Screws are therefore by convention right handed.
One final remark before leaving vector products. We noted above that scalar products and vector products are closely connected to the notions of length and area, but mathematics per se need not specify the units of the quantities multiplied in a product (that is the province of physics, as we shall see). We have numerous examples where two different kinds of vectors (with different units but referred to a common coordinate system for direction) are multiplied together with one or the other of these products. In actual fact, there often is a buried squared length or area (which we now agree are different kinds of numbers) in those products, but it won't always be obvious in the dimensions of the result.
Two of the most important uses of the scalar and vector product are to define the work done as the force through a distance (using a scalar product as work is a scalar quantity) and the torque exerted by a force applied at some distance from a center of rotation (using a vector product as torque is an axial vector). These two quantities (work and torque) have the same units and yet are very different kinds of things. This is just one example of the ways geometry, algebra, and units all get mixed together in physics.
At first this will be very confusing, but remember, back when you where in third grade multiplying integer numbers was very confusing and yet rational numbers, irrational numbers, general real numbers, and even complex numbers were all waiting in the wings. This is more of the same, but all of the additions will mean something and have a compelling beauty that comes out as you study them. Eventually it all makes very, very good sense.