Complex Numbers

This is a very terse review of their most important properties. An arbitrary complex number $z$ can be written as:

$$z = x + i y$$ (4.1)

$$= \vert z\vert \cos(\theta) + i \vert z\vert \sin(\theta)$$ (4.2)

$$= \vert z\vert e^{i\theta}$$ (4.3)

where $x = \vert z\vert\cos(\theta)$, $y = \vert z\vert\sin(\theta)$, and $\vert z\vert = \sqrt{x^2 + y^2}$. All complex numbers can be written as a real amplitude $\vert z\vert$ times a complex exponential form involving a phase angle. Again, it is difficult to convey how incredibly useful this result is without further study, but I commend it to your attention.

There are a number of really interesting properties that follow from the exponential form. For example, consider multiplying two complex numbers $a$ and $b$:

$$a = \vert a\vert e^{i\theta_a} = \vert a\vert\cos(\theta_a) + i\vert a\vert\sin(\theta_a)$$ (4.4)

$$b = \vert b\vert e^{i\theta_b} = \vert b\vert\cos(\theta_b) + i\vert b\vert\sin(\theta_b)$$ (4.5)

$$a b = \vert a\vert\vert b\vert e^{i(\theta_a + \theta_b)}$$ (4.6)

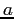and we see that multiplying two complex numbers multiplies their amplitudes and adds their phase angles. Complex multiplication thus rotates and rescales numbers in the complex plane.