Next: Math References Up: Mathematical Physics Previous: Cylindrical Contents

The Dirac $\delta$ -Function

delta-function.eps

The Dirac $\delta$ -function is usually defined to be a convenient (smooth, integrable, narrow) distribution e.g. $\chi(x)$ that is symmetric and peaked in the middle and with a parametric width $\Delta x$ . The distribution is normalized (in terms of its width) so that its integral is one:

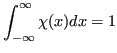
$\displaystyle \int_{-\infty}^{\infty} \chi(x) dx = 1$

One then takes the limit $\Delta x \to 0$ while continuing to enforce the normalization condition to define the $\delta$ -function:

$\displaystyle \delta(x) = \lim_{\Delta x \to 0} \chi(x)$

The $\delta$ -function itself is thus not strictly speaking a ``function'', but rather the limit of a distibution. Furthermore, it is nearly useless in and of itself - as a ``function'' standing alone it can be thought of as an infinitely narrow, infinitely high peak around with a conserved area of unity. It's primary purpose in physics is to be multiplied by an actual function and integrated, with the $\Delta x \to 0$ limit taken after doing the integral. However, the result of applying this process is general, and useful enough to be treated as a standalone and reusable set of integral definitions and rules.

Here are its principle definitions and properties:

Integration against a function:

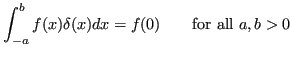
$\displaystyle \int_{-a}^b f(x)\delta(x) dx = f(0) \quad\quad\textrm{for all } a,b>0$
Displacement of the $\delta$ -function:

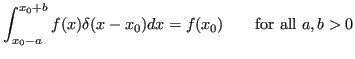
$\displaystyle \int_{x_0 - a}^{x_0 + b} f(x) \delta(x - x_0) dx = f(x_0) \quad\quad\textrm{for all } a,b>0$
-substitution ( ):

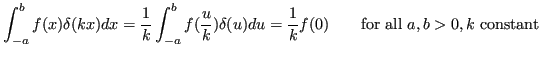
$\displaystyle \int_{-a}^b f(x)\delta(kx) dx = \frac{1}{k} \int_{-a}^b f(\frac{u... ...) du = \frac{1}{k} f(0) \quad\quad\textrm{for all } a,b>0, k\textrm{ constant}$
Integration by parts/derivative of a $\delta$ -function:

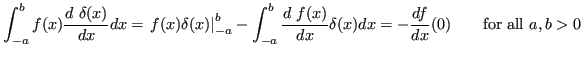
$\displaystyle \int_{-a}^b f(x)\frac{d\ \delta(x)}{dx} dx = \left.f(x)\delta(x)\... ...\ f(x)}{dx}\delta(x) dx = - \frac{df}{dx}(0) \quad\quad\textrm{for all } a,b>0$

(the $\delta$ -function is zero everywhere but at so the first term in integration by parts vanishes).
The 3-D $\delta$ -function:

$\displaystyle \delta(\vr) = \delta(x)\delta(y)\delta(z)$

such that:

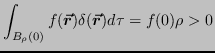
$\displaystyle \int_{B_\rho(0)} f(\vr)\delta(\vr) d\tau = f(0) \rho>0$

Note: $B_\rho(0)$ stands for the open ball of radius &rho#rho; in the neighborhood of = 0. More properly, the result holds for any integration volume that contains an open ball of at least infinitesimal radius around the origin.
This result can also be displaced:

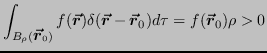
$\displaystyle \int_{B_\rho(\vr_0)} f(\vr)\delta(\vr - \vr_0) d\tau = f(\vr_0) \rho>0$

as long as the integration volume (now) contains an open ball around $\vr_0$ .
A warning: When one tries to build a $\delta$ -function in two or three dimensions in curvilinear coordinates, you need to take into account the appropriate terms in the Jacobian (or think about the chain rule, if you prefer). These are just the discussed extensively above. For spherical coordinates, then:

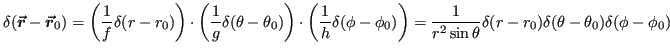
$\displaystyle \delta(\vr - \vr_0) = \left(\frac{1}{f}\delta(r - r_0)\right)\cdo... ...1}{r^2\sin\theta}\delta(r - r_0)\delta(\theta - \theta_0)\delta(\phi - \phi_0)$

This selectively cancels the product in the volume element:

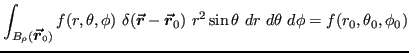
$\displaystyle \int_{B_\rho(\vr_0)} f(r,\theta,\phi)\ \delta(\vr - \vr_0)\ r^2 \sin\theta\ dr\ d\theta\ d\phi = f(r_0,\theta_0,\phi_0)$

as expected. Similarly in cylindrical coordinates:

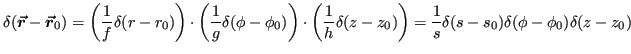
$\displaystyle \delta(\vr - \vr_0) = \left(\frac{1}{f}\delta(r - r_0)\right)\cdo... ...z-z_0)\right) = \frac{1}{s}\delta(s - s_0)\delta(\phi - \phi_0)\delta(z - z_0)$