


Next: 4-Vectors
Up: Special Relativity
Previous: Einstein's Postulates
Contents
To motivate the Lorentz transformation, recall the Galilean
transformation between moving coordinate systems:
 |
 |
 |
(17.1) |
 |
 |
 |
(17.2) |
 |
 |
 |
(17.3) |
 |
 |
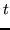 |
(17.4) |
(where 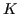 is fixed and
is fixed and 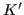 is moving in the 1-direction at speed
is moving in the 1-direction at speed  ).
).
Then
 |
(17.5) |
or Newton's Laws are covariant with respect to the Gallilean
transformation.
But
 |
(17.6) |
and so
 |
 |
 |
(17.7) |
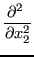 |
 |
 |
(17.8) |
 |
 |
 |
(17.9) |
 |
 |
 |
(17.10) |
Thus if
 |
(17.11) |
then
 |
(17.12) |
(!) so that the wave equation, and hence Maxwell's equations which lead
directly to the wave equation in free space, are not covariant with
respect to the Gallilean transformation! They already determine the
permitted velocity of a light wave, and do not allow that velocity to depend
on anything but the properties of the medium through which the wave is
transmitted.
The simplest linear transformation of coordinates is that preserves the form
of the wave equation is easy to determine. It is one that keeps the speed of
the (light) wave equal in both the 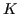 and the
and the 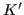 frames. Geometrically, if
a flash of light is emitted from the (coincident) origins at time
frames. Geometrically, if
a flash of light is emitted from the (coincident) origins at time
 , it will appear to expand like a sphere out from both coordinate
origins, each in its own frame:
, it will appear to expand like a sphere out from both coordinate
origins, each in its own frame:
 |
(17.13) |
and
 |
(17.14) |
are simultaneous constraints on the equations. Most generally,
![$\displaystyle (ct)^2 - (x^2 + y^2 + z^2) = \lambda^2 \left[ (ct')^2 - (x'^2 + y'^2 + z'^2) \right ]$](img1509.png) |
(17.15) |
where,
 describes a possible change of scale between the
frames. If we insist that the coordinate transformation be homogeneous and
symmetric between the frames17.1, then
describes a possible change of scale between the
frames. If we insist that the coordinate transformation be homogeneous and
symmetric between the frames17.1, then
 |
(17.16) |
Let us define
 |
 |
 |
(17.17) |
 |
 |
 |
(17.18) |
 |
 |
 |
(17.19) |
 |
 |
 |
(17.20) |
 |
 |

Minkowski metric |
(17.21) |
Then we need a linear transformation of the coordinates that mixes x and (ct) in the direction of  in such a way that the length
in such a way that the length
 |
(17.22) |
is conserved and that goes into the Gallilean transformation as  . If we continue to assume that
. If we continue to assume that  is in the 1 direction, this leads to
the Lorentz transformation:
is in the 1 direction, this leads to
the Lorentz transformation:
 |
 |
 |
(17.23) |
 |
 |
 |
(17.24) |
 |
 |
 |
(17.25) |
 |
 |
 |
(17.26) |
where at  ,
,
 |
(17.27) |
Then
 |
(17.28) |
leads to
 |
(17.29) |
or
 |
(17.30) |
so
 |
(17.31) |
where we choose the  sign by convention. This makes
sign by convention. This makes
 . Finally,
. Finally,
 |
(17.32) |
as we all know and love.
Now, let me remind you that when  ,
,
 |
(17.33) |
to lowest surviving order in
 . As we shall see, this is why
``kinetic energy'' in non-relativistic systems (being defined as the total
energy minus the potential energy and the rest mass energy) is the usual
. As we shall see, this is why
``kinetic energy'' in non-relativistic systems (being defined as the total
energy minus the potential energy and the rest mass energy) is the usual
 .
.
The inverse transformation (from 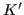 to
to 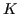 ) is also of some interest.
) is also of some interest.
 |
 |
 |
(17.34) |
 |
 |
 |
(17.35) |
 |
 |
 |
(17.36) |
 |
 |
 |
(17.37) |
which is perfectly symmetric, with  . It appears that which frame is
at ``rest'' and which is moving is mathematically, at least, a matter of
perspective.
. It appears that which frame is
at ``rest'' and which is moving is mathematically, at least, a matter of
perspective.
Finally, if we let
 |
(17.38) |
(in an arbitrary direction) then we have but to use dot products to align the
vector transformation equations with this direction:
x_0' & = & &gamma#gamma;(x_0 - &beta#beta; ·x)
x' & = & x + &gamma#gamma;- 1&beta#beta;^2 (&beta#beta; ·
x) &beta#beta; - &gamma#gamma;&beta#beta; x_0
I think that you should prove that this is correct as an exercise. Since the
direction of
 is arbitrary, it should suffice to show that this
reduces the the form above for that direction and an arbitrary transverse
direction.
is arbitrary, it should suffice to show that this
reduces the the form above for that direction and an arbitrary transverse
direction.
Solution:
Note that
x_&par#parallel;= (&beta#beta; ·x)&beta#beta;&beta#beta;^2
Lorentz transform it according to this rule and one gets (by inspection)
x_&par#parallel;' = &gamma#gamma;(x_&par#parallel;- &beta#beta; x_0)
as one should. The  transform is obvious. Finally, the other two
(
transform is obvious. Finally, the other two
( ) components do not get a contribution from
) components do not get a contribution from 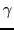 . That is,
x' = (x_&perp#perp;+ x_&par#parallel;) + &gamma#gamma;x_&par#parallel;
- x_&par#parallel;- &gamma#gamma;&beta#beta; x_0
(reconstructing the result above directly) QED.
. That is,
x' = (x_&perp#perp;+ x_&par#parallel;) + &gamma#gamma;x_&par#parallel;
- x_&par#parallel;- &gamma#gamma;&beta#beta; x_0
(reconstructing the result above directly) QED.
This is not the most general or convenient way to write the final transform.
This is because 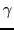 and
and  are both related functions; it should
not be necessary to use two parameters that are not independent. Also, the
limiting structure of the transformation is not at all apparent without
considering the functional forms in detail.
are both related functions; it should
not be necessary to use two parameters that are not independent. Also, the
limiting structure of the transformation is not at all apparent without
considering the functional forms in detail.
It is easy to see from the definition above that
(&gamma#gamma;^2 - &gamma#gamma;^2 &beta#beta;^2) = 1.
The range of  is determined by the requirement that the transformation
be non-singular and its symmetry:
0 &le#le;&beta#beta;< 1 so that 1 &le#le;&gamma#gamma;< &infin#infty;.
If we think about functions that ``naturally'' parameterize these ranges, they
are:
^2 &xi#xi;- ^2 &xi#xi;= 1
where
&beta#beta;& = & &xi#xi; = e^-&xi#xi; - e^&xi#xi;e^-&xi#xi; +
e^&xi#xi; &isin#in; [0,1)
is determined by the requirement that the transformation
be non-singular and its symmetry:
0 &le#le;&beta#beta;< 1 so that 1 &le#le;&gamma#gamma;< &infin#infty;.
If we think about functions that ``naturally'' parameterize these ranges, they
are:
^2 &xi#xi;- ^2 &xi#xi;= 1
where
&beta#beta;& = & &xi#xi; = e^-&xi#xi; - e^&xi#xi;e^-&xi#xi; +
e^&xi#xi; &isin#in; [0,1)
&gamma#gamma;& = & &xi#xi; = 12 (e^-&xi#xi; + e^&xi#xi;)
&isin#in; [1,&infin#infty;)
&gamma#gamma;&beta#beta;& = & &xi#xi; = 12 (e^-&xi#xi; -
e^&xi#xi;) &isin#in; [0,&infin#infty;) .
The parameter 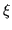 is called the boost parameter or rapidity.
You will see this used frequently in the description of relativistic problems.
You will also hear about ``boosting'' between frames, which essentially means
performing a Lorentz transformation (a ``boost'') to the new frame. This will
become clearer later when we generalize these results further. To give you
something to meditate upon, consider in your minds the formal similarity
between a ``boost'' and a ``rotation'' between the
is called the boost parameter or rapidity.
You will see this used frequently in the description of relativistic problems.
You will also hear about ``boosting'' between frames, which essentially means
performing a Lorentz transformation (a ``boost'') to the new frame. This will
become clearer later when we generalize these results further. To give you
something to meditate upon, consider in your minds the formal similarity
between a ``boost'' and a ``rotation'' between the
 and
and
 coordinates where the rotation is through an imaginary angle
coordinates where the rotation is through an imaginary angle  .
Hmmmm.
.
Hmmmm.
To elucidate this remark a wee tad more, note that in this parameterization,
x_0' & = & x_0 &xi#xi;- x_&par#parallel;&xi#xi;
x_&par#parallel;' & = & -x_0 &xi#xi;+ x_&par#parallel;&xi#xi;
x_&perp#perp;' & = & x_&perp#perp;.
What is the
 transformation matrix (in four dimensions)
for this result? Does it look like a ``hyperbolic rotation''17.2 or what?
transformation matrix (in four dimensions)
for this result? Does it look like a ``hyperbolic rotation''17.2 or what?
We have just determined that the (vector) coordinate system transforms a
certain way. What, then, of vector fields, or any other vector quantity? How
do general vectors transform under a boost? This depends on the nature of the
vectors. Many vectors, if not most, transform like the underlying coordinate
description of the vectors. This includes the ones of greatest interest in
physics. To make this obvious, we will have to generalize a vector quantity
to four dimensions.



Next: 4-Vectors
Up: Special Relativity
Previous: Einstein's Postulates
Contents
Robert G. Brown
2017-07-11
![]() is fixed and
is fixed and ![]() is moving in the 1-direction at speed
is moving in the 1-direction at speed ![]() ).
).




![]() and the
and the ![]() frames. Geometrically, if
a flash of light is emitted from the (coincident) origins at time
frames. Geometrically, if
a flash of light is emitted from the (coincident) origins at time
![]() , it will appear to expand like a sphere out from both coordinate
origins, each in its own frame:
, it will appear to expand like a sphere out from both coordinate
origins, each in its own frame:
![]() in such a way that the length
in such a way that the length


![]() ,
,

![]() to
to ![]() ) is also of some interest.
) is also of some interest.
![]() transform is obvious. Finally, the other two
(
transform is obvious. Finally, the other two
(![]() ) components do not get a contribution from
) components do not get a contribution from ![]() . That is,
x' = (x_&perp#perp;+ x_&par#parallel;) + &gamma#gamma;x_&par#parallel;
- x_&par#parallel;- &gamma#gamma;&beta#beta; x_0
(reconstructing the result above directly) QED.
. That is,
x' = (x_&perp#perp;+ x_&par#parallel;) + &gamma#gamma;x_&par#parallel;
- x_&par#parallel;- &gamma#gamma;&beta#beta; x_0
(reconstructing the result above directly) QED.
![]() and
and ![]() are both related functions; it should
not be necessary to use two parameters that are not independent. Also, the
limiting structure of the transformation is not at all apparent without
considering the functional forms in detail.
are both related functions; it should
not be necessary to use two parameters that are not independent. Also, the
limiting structure of the transformation is not at all apparent without
considering the functional forms in detail.
![]() is determined by the requirement that the transformation
be non-singular and its symmetry:
0 &le#le;&beta#beta;< 1 so that 1 &le#le;&gamma#gamma;< &infin#infty;.
If we think about functions that ``naturally'' parameterize these ranges, they
are:
^2 &xi#xi;- ^2 &xi#xi;= 1
where
&beta#beta;& = & &xi#xi; = e^-&xi#xi; - e^&xi#xi;e^-&xi#xi; +
e^&xi#xi; &isin#in; [0,1)
is determined by the requirement that the transformation
be non-singular and its symmetry:
0 &le#le;&beta#beta;< 1 so that 1 &le#le;&gamma#gamma;< &infin#infty;.
If we think about functions that ``naturally'' parameterize these ranges, they
are:
^2 &xi#xi;- ^2 &xi#xi;= 1
where
&beta#beta;& = & &xi#xi; = e^-&xi#xi; - e^&xi#xi;e^-&xi#xi; +
e^&xi#xi; &isin#in; [0,1)
![]() is called the boost parameter or rapidity.
You will see this used frequently in the description of relativistic problems.
You will also hear about ``boosting'' between frames, which essentially means
performing a Lorentz transformation (a ``boost'') to the new frame. This will
become clearer later when we generalize these results further. To give you
something to meditate upon, consider in your minds the formal similarity
between a ``boost'' and a ``rotation'' between the
is called the boost parameter or rapidity.
You will see this used frequently in the description of relativistic problems.
You will also hear about ``boosting'' between frames, which essentially means
performing a Lorentz transformation (a ``boost'') to the new frame. This will
become clearer later when we generalize these results further. To give you
something to meditate upon, consider in your minds the formal similarity
between a ``boost'' and a ``rotation'' between the
![]() and
and
![]() coordinates where the rotation is through an imaginary angle
coordinates where the rotation is through an imaginary angle ![]() .
Hmmmm.
.
Hmmmm.
![]() transformation matrix (in four dimensions)
for this result? Does it look like a ``hyperbolic rotation''17.2 or what?
transformation matrix (in four dimensions)
for this result? Does it look like a ``hyperbolic rotation''17.2 or what?