


Next: The Hansen Multipoles
Up: Vector Multipoles
Previous: Magnetic and Electric Multipoles
Contents
Recall that
 |
(14.34) |
This is an ``orbital'' rotation operator. In systems with spin it is more
convenient in many cases to define a ``total'' rotation operator that adds the
orbital rotation operator to a ``spin'' rotation operator (defined below).
Since total angular momentum (as opposed to orbital angular momentum) is a
relativistically invariant quantity that appears ``naturally'' in covariant
kinematics, we are inspired to find a representation that is
- A vector function of its coordinates.
- Simultaneous eigenfunctions of
 ,
, 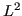 , and
, and  .
.
- Possessed of certain desirable properties we will derive.
Actually, figuring out something like this the first time is not quite so
easy; it is full of false starts and exploring alternatives. After the fact,
however, it is clear that this is the correct choice. It is also extremely
useful in quantum theory.
The total rotation operator is
 |
(14.35) |
where
 |
(14.36) |
is the ``spin'' operator.
Aside: The Spin Operator
S in this expression is a tensor operator. It (like all
operators) has no meaning by itself. It is, however, quite different from the
scalar operators you are used to. Among other things, when S operates
on a vector A, it generates a new vector that points in a different direction. Let us see this.
In the definition of S, I is the identity tensor (unit diagonal
matrix) and it is crossed into whatever sits on its right. To understand its
action, let us evaluate its cartesian components acting on some vector A:
or (e. g.)
 |
(14.40) |
Note that the action of a component of S on a vector A shifts the
direction of A to a direction perpendicular to both S and the
component. Only by considering the action of all the components can the total
vector action of S on A in a given direction be evaluated.
There are several important properties of S. The first is to note that
it has the form of an angular momentum operator with a special action on
vectors. If we form  and evaluate its action on A:
and evaluate its action on A:
for  .
.  acting on any vector produces 2 times the same
vector, telling us that a vector has ``spin angular momentum'' of 1. Note
that this connection is universal. In field theory a ``vector boson'' has
spin 1. In electrodynamics (quantum or classical) the ``vector radiation
field'' has spin one.
acting on any vector produces 2 times the same
vector, telling us that a vector has ``spin angular momentum'' of 1. Note
that this connection is universal. In field theory a ``vector boson'' has
spin 1. In electrodynamics (quantum or classical) the ``vector radiation
field'' has spin one.
The spin operator thus formed is more general, because its action can be
extended to higher rank tensors. (2nd rank tensor) gravitational fields have
spin 2. Scalar (0th rank tensor) fields have spin 0. To treat more general
cases, however, we have to work with tensor indices explicitly and you'll see
enough of that in the section on relativity. Feel free to study this matter
further. Louck and Biedenharn's book (Encycl. of Math Phys., see me for ref.)
contains a much deeper discussion of this entire subject.
It may seem that with such a peculiar structure,  can have no
eigenvectors. This is not the case. You should verify that
can have no
eigenvectors. This is not the case. You should verify that
are eigenvectors such that
 |
(14.45) |
for
 and
and
 |
(14.46) |
for  . You should also verify the commutation relations for the
components of S, that is, show that
. You should also verify the commutation relations for the
components of S, that is, show that
 |
(14.47) |
making it a ``true'' rotation/angular momentum operator.
In addition, we will need to use the operators
 |
(14.48) |
 |
(14.49) |
(etc.) and
 |
(14.50) |
so that
 |
(14.51) |
which can be proven as follows.
Consider its action on A (as usual):
where the meaning of the latter expression is hopefully now clear.
Then we define the vector spherical harmonics
 by:
by:
Note that in order for the latter expression to be true, we might reasonably
expect the vector spherical harmonics to be constructed out of sums of
products of spherical harmonics and the eigenvectors of the operator  defined above. This is the vector analogue of constructing a spinor
wavefunction in quantum theory.
defined above. This is the vector analogue of constructing a spinor
wavefunction in quantum theory.
In addition, we normalize these orthogonal functions so that they are orthonormal as a dot product. This will allow us to use them to
construct projections.
 |
(14.56) |
We now need to derive the properties of these functions. We begin by applying
 to
to

 |
(14.57) |
so that we get
 |
(14.58) |
Most of the later results will be based on this one, so understand it
completely.
If we take
 of both sides of (14.62), use a vector
identity and recall that
of both sides of (14.62), use a vector
identity and recall that
 we get:
we get:
![$\displaystyle [j(j+1) - \ell(\ell+1)] {\bf L} \cdot \vsh{j,\ell}{m} = 0.$](img1264.png) |
(14.59) |
Similarly, we form the vector product of L with both sides of
(14.62):
 |
(14.60) |
To reduce this further, we must use the operator vector identity (which you
should prove)
 |
(14.61) |
and eliminate the
 using (14.62). One gets:
using (14.62). One gets:
If we eliminate the
 (using the result above) we get
the characteristic equation that is a constraint on the possible values
of
(using the result above) we get
the characteristic equation that is a constraint on the possible values
of  and
and  :
:
 |
(14.63) |
where
 |
(14.64) |
by definition. The solutions to this factorizable cubic are:
We only need to consider the solutions with positive  in this problem as
the others are not independent in this case. Since
in this problem as
the others are not independent in this case. Since
 we only need
consider the first three possibilities.
we only need
consider the first three possibilities.
Solutions with 
Then  and
and
 |
(14.65) |
from the third equation above. If we take the dot product of L with
this relation, we get
 |
(14.66) |
and we thus see that
 and so:
and so:
 |
(14.67) |
(!) where we have normalized the result.
We have at last found something
recognizable. This is precisely the combination of spherical harmonics and
L we found in our brief excursion into multipoles! We see that we could
have written the (e. g.) magnetic solution as
With just a little more work (later) we will be able to obtain the curl part
as a general result, which will really simplify life for us. It is a
trivial exercise (left for the reader) to verify that
 |
(14.70) |
One simply plugs in the explicit form of  and commutes the resultant
and commutes the resultant
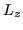 with L to cancel the ``spin'' part.
with L to cancel the ``spin'' part.
Solutions with

If
 , we see from the equation after (14.62) that
, we see from the equation after (14.62) that
 . To go further we have to go back to (14.62) and
follow a different line. If we multiply both sides by
. To go further we have to go back to (14.62) and
follow a different line. If we multiply both sides by
 and
and
 ,
,
![$\displaystyle \left [j(j+1) - \ell(\ell+1) -2 \right ] \hat{r} \cdot \vsh{j \ell}{m} = 2i \hat{r} \cdot {\bf L} \times \vsh{j \ell}{m}$](img1288.png) |
(14.71) |
and
![$\displaystyle \left [j(j+1) - \ell(\ell+1) -2 \right ] \hat{r} \times \vsh{j \ell}{m} = 2i \hat{r} \times ({\bf L} \times \vsh{j \ell}{m})$](img1289.png) |
(14.72) |
We can reduce these with the vector identities
 |
(14.73) |
and
 |
(14.74) |
You should get
![$\displaystyle \left [ j(j+1) - \ell(\ell+1) + 2 \right ] \hat{r} \cdot \vsh{j \ell}{m} = -2i {\bf L} \cdot (\hat{r} \times \vsh{j \ell}{m})$](img1292.png) |
(14.75) |
and
![$\displaystyle \left [ j(j+1) - \ell(\ell+1) \right ] \hat{r} \times \vsh{j \ell}{m} = 2i {\bf L} (\hat{r} \cdot \vsh{j \ell}{m}).$](img1293.png) |
(14.76) |
Finally, if we plug the second of these into the first and eliminate the cross
product, we get the scalar equation:
![$\displaystyle \frac{1}{4} \left [ j(j+1) - \ell(\ell+1) \right ] \left [ j(j+1)...
...right ] (\hat{r} \cdot \vsh{j \ell}{m}) = L^2 (\hat{r} \cdot \vsh{j \ell}{m}) .$](img1294.png) |
(14.77) |
This implies that
 is a spherical harmonic:
that is a constant
is a spherical harmonic:
that is a constant
 . What? This is not obvious to you?
Well, just this once:
. What? This is not obvious to you?
Well, just this once:
![$\displaystyle \left [ \frac{j(j+1) - \ell(\ell+1)}{2} \right] \left [ \frac{j(j+1) - \ell(\ell + 1)}{2} + 1 \right ] = k(k+1)$](img1297.png) |
(14.78) |
This has the solutions
-
![$ k = \left [ \frac{j(j+1) - \ell(\ell+1)}{2} \right ]$](img1298.png)
-
![$ k = \left [ \frac{j(j+1) - \ell(\ell+1)}{2} \right ] - 1$](img1299.png) .
.
Since we already know that
 , we can investigate these two
cases explicitly. The positive solutions (in both cases) are easily seen to
be
, we can investigate these two
cases explicitly. The positive solutions (in both cases) are easily seen to
be  . We can then construct the complete solutions, since
. We can then construct the complete solutions, since
 |
(14.79) |
is an identity (related to the symmetric/antisymmetric decomposition and hence
worth proving) and since we have already shown that
![$\displaystyle \hat{r} \times \vsh{j,\ell}{m} = 2 i \left[ j(j+1) - \ell(\ell + 1) \right ]^{-1} {\bf L} (\hat{r} \cdot \vsh{j,\ell}{m})$](img1303.png) |
(14.80) |
with
 a constant times
a constant times
 . We get:
. We get:
![$\displaystyle \vsh{j,\ell}{m} = (constant) \left \{ \hat{r} - 2i [j(j+1) - \ell(\ell+1)]^{-1} (\hat{r} \times {\bf L}) \right \} Y_{\ell,m} .$](img1305.png) |
(14.81) |
An exercise will be to verify the normalization of the final solutions:
You must also verify that they satisfy the equation for  .
.
Finally, you are probably wondering why we have bothered to learn all of this
about the
 cases in the first place. It is because
cases in the first place. It is because
The action of the curl mixes the vector spherical harmonics. In fact,
it acts to shift  by one in any permitted direction (see handout sheet).
Therefore, in order to evaluate the entire EM field and express it compactly,
one must use the notation of the vector spherical harmonics. You should prove
this, and at leat one of the divergence equations for homework. You will need
to get the components of the v.s.h. along and transverse to
by one in any permitted direction (see handout sheet).
Therefore, in order to evaluate the entire EM field and express it compactly,
one must use the notation of the vector spherical harmonics. You should prove
this, and at leat one of the divergence equations for homework. You will need
to get the components of the v.s.h. along and transverse to  in order
to do the vector algebra.
in order
to do the vector algebra.
This is not too bad, but (as we shall see) it is not the best we can do. By
carefully defining a particular set of multipolar solutions, we can make our
notation itself do almost all the work of doing the curls, etc. so that all
we have to do at either end is translate a paticular problem into and out of
the notation with the formal solution in hand. Next time we will do just that
as we develop the Hansen Multipolar Solutions.



Next: The Hansen Multipoles
Up: Vector Multipoles
Previous: Magnetic and Electric Multipoles
Contents
Robert G. Brown
2017-07-11
![]() and evaluate its action on A:
and evaluate its action on A:
![]() can have no
eigenvectors. This is not the case. You should verify that
can have no
eigenvectors. This is not the case. You should verify that


![]() by:
by:

![]() to
to
![]()
![]() of both sides of (14.62), use a vector
identity and recall that
of both sides of (14.62), use a vector
identity and recall that
![]() we get:
we get:
![]() (using the result above) we get
the characteristic equation that is a constraint on the possible values
of
(using the result above) we get
the characteristic equation that is a constraint on the possible values
of ![]() and
and ![]() :
:
![]()
![]() and
and


![]()
![]() , we see from the equation after (14.62) that
, we see from the equation after (14.62) that
![]() . To go further we have to go back to (14.62) and
follow a different line. If we multiply both sides by
. To go further we have to go back to (14.62) and
follow a different line. If we multiply both sides by
![]() and
and
![]() ,
,
![$\displaystyle \frac{1}{4} \left [ j(j+1) - \ell(\ell+1) \right ] \left [ j(j+1)...
...right ] (\hat{r} \cdot \vsh{j \ell}{m}) = L^2 (\hat{r} \cdot \vsh{j \ell}{m}) .$](img1294.png)
![]() is a spherical harmonic:
that is a constant
is a spherical harmonic:
that is a constant
![]() . What? This is not obvious to you?
Well, just this once:
. What? This is not obvious to you?
Well, just this once:
![$\displaystyle \left [ \frac{j(j+1) - \ell(\ell+1)}{2} \right] \left [ \frac{j(j+1) - \ell(\ell + 1)}{2} + 1 \right ] = k(k+1)$](img1297.png)
![]() , we can investigate these two
cases explicitly. The positive solutions (in both cases) are easily seen to
be
, we can investigate these two
cases explicitly. The positive solutions (in both cases) are easily seen to
be ![]() . We can then construct the complete solutions, since
. We can then construct the complete solutions, since
![$\displaystyle - \frac{1}{\sqrt{j(2j+1)}} [-j \hat{r} + i \hat{r}
\times {\bf L}] Y_{\ell,m}$](img1307.png)
![$\displaystyle - \frac{1}{\sqrt{(j+1)(2j+1)}} [(j+1)\hat{r} + i
\hat{r} \times {\bf L}] Y_{\ell,m}.$](img1309.png)
![]() cases in the first place. It is because
cases in the first place. It is because
![$\displaystyle \sqrt{\frac{j+1}{2j+1}}
\Big[(j+1) \frac{f}{r} + \frac{df}{dr}\Big] \vsh{j,j-1}{m} \hfill$](img1311.png)
![$\displaystyle \quad \quad + \quad \sqrt{\frac{j}{2j+1}} \Big[-j \frac{f}{r} +
\frac{df}{dr} \Big] \vsh{j,j+1}{m} .$](img1312.png)