Real Numbers

Real numbers are of obvious importance in physics, and electrodynamics is no exception. Measured or counted quantities are almost invariably described in terms of real numbers or their embedded cousins, the integers. Their virtue in physics comes from from the fact that they form a (mathematical) fieldField_mathematics; that is, they support the mathematical operations of addition, subtraction, multiplication and division, and it empirically turns out that physical laws turn out to be describable in terms of algebraic forms based on (at least) real numbers. Real numbers form a group under ordinary multiplication and, because multiplication is associative and each element possesses a unique inverse, they form a division algebraDivision_algebra.

A division algebra is one where any element other than zero can be divided into any other element to produce a unique element. This property of real numbers is extremely important - indeed it is the property that makes it possible to use algebra per se to solve for many physical quantities from relations expressed in terms of products and sums. The operational steps: b ·c & = & a
(b ·c)·c^-1 & = & a ·c^-1
b ·(c ·c^-1) & = & a ·c^-1
b = b ·1 & = & a ·c^-1 are so pervasively implicit in our algebraic operations because they are all learned in terms of real numbers that we no longer even think about them until we run into them in other contexts, for example when $a, b, c$ are matrices, with at least 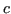$c$ being an invertible matrix.

In any event real numbers are ideally suited for algebra because they form a field, in some sense the archetypical field, whereby physical law can be written down in terms of sums and products with measurable quantities and physical parameters represented by real numbers. Other fields (or rings) are often defined in terms of either subsets of the real numbers or extensions of the real numbers, if only because when we write a symbol for a real number in an algebraic computation we know exactly what we can and cannot do with it.

Real numbers are the basis of real ``space'' and ``time'' in physics - they are used to form an algebraic geometry wherein real numbers are spatiotemporal coordinates. This use is somewhat presumptive - spacetime cannot be probed at distances shorter than the Planck length ( $1.616 \times 10^{-35}$ meters) - and may be quantized and granular at that scale. Whatever this may or may not mean (close to nothing, lacking a complete quantum theory of gravity) it makes no meaningful difference as far as the applicability of e.g. calculus down to that approximate length scale, and so our classical assumption of smooth spacetime will be quite reasonable.

Are real numbers sufficient to describe physics, in particular classical electrodynamics? The answer may in some sense be yes (because classical measurable quantities are invariably real, as are components of e.g. complex numbers) but as we will see, it will be far easier to work over a different field: complex numbers, where we will often view real numbers as just the real part of a more general complex number, the real line as just one line in a more general complex plane. As we will see, there is a close relationship between complex numbers and a two-dimensional Euclidean plane that permits us to view certain aspects of the dynamics of the real number valued measurable quantities of physics as the real projection of dynamics taking place on the complex plane. Oscillatory phenomena in general are often viewed in this way.