What Is the Eightfold Way?
Many attempts have been made in trying to discover a system of organization that grouped elementary particles into larger groups of identification. The only one that has had much success is the Eightfold Way. Proposed independently in 1961 by both Murray Gell-Mann and Yuval Ne'eman, the Eightfold Way groups the baryons and mesons into geometrical patterns of the same baryon number, spin and parity. An example of one of these shapes is the baryon octet which consists of the eight lightest baryons.
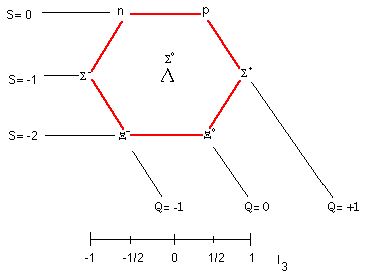
Notice how the particles are arranged in a hexagonal form with two baryons in the center. Each of these baryons has a baryon number of one, a spin of one-half and positive parity. Also note that in the Eightfold Way, strangeness (S) is plotted horizontally and the quantum number (I3) is plotted vertically. The symmetry of charge (Q) along the diagonal of the figure develops just by plotting strangeness versus quantum number. Not only does a neat geometric shape appear, but charge automatically develops into a perfect symmetry as well.
These groups, from the SU(3) symmetry group of the Lie groups developed Sophus Lie, are the result of combining smaller groups of hadrons called multiplets. Multiplets combine particles of like mass and like interaction capabilities that only differ in charge into a common group. Looking back at the diagram we see that the neutron and proton, the sigma minus, sigma zero and sigma plus, and the xi minus and xi zero are three different multiplets that are closely connected in the supermultiplet horizontally.
What Can the Eightfold Way Do?
From knowing the SU(3) symmetry grouping, relationships between the masses are found. Two such equations that do so are the Gell-Mann--Okubo and the Coleman--Glashow equations which for the above baryons state the following:
m(n) + m(
m(
Similar equations are easily obtained from other octets by using each particle's position in the figure and replacing it with those particles found in the corresponding position in this octet. These are two of the relationships that helped to verify the Eightfold Way since none of the supermultiplets had been completely filled upon its discovery. However, the discovery of the -minus particle was the main factor in proving the validity of the Eightfold Way. The -minus was thought to be a part of the following decuplet of "heavy" baryons as it is in its current position below.
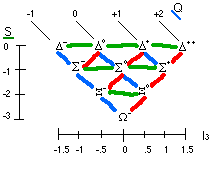
Using the Eightfold Way, the -minus mass (1672 MeV), spin (3/2), strangeness (-3), quantum number (0), and charge (-1) were accurately predicted. How is this possible? The axes on the graph predict what quantum number and strangeness the particle would have in order to be in that position. Then noticing the pattern in the orientation of the distribution of charge and noting that most of the particles in the decuplet have the same spin, these two properties were fairly easy to predict. Mass of the -minus followed easily as well when it was noticed that the average mass of the first row across is 1232 MeV, the second row 1385 MeV, and the third row 1530 MeV. The predicted value was then about 1675 MeV since it appears that moving down one row increases the mass by 145 MeV.
Also, note again that the Eightfold Way combines multiplets of particles of like mass and interactive capabilities in the same horizontal row.
Another observation made via the Eightfold Way is the origin of the strong force. Found within this model, it is seen that like the electric force that consists of two charges and potentially one carrier particle (photon), the strong force consists of a much more complicated system of several charges and eight carrier particles.
Is This Relevant to Current Knowledge?
The answer to this question is a definite "yes!" Gell-Mann continued his studies in his model and independently of Zweig, these two gentlemen proposed that each of the particles in the geometric figures could be composed of three basic particles. These three particles could form each larger composite particle by combining in various ways within the symmetry of a triplet. These particles were first called quarks by Gell-Mann when he proposed this model. Today it is believed that there are more than three quark--anti quark pairs, but at the time the idea was brand-new. Gell-Mann's idea can in one instance be seen as the building blocks for the baryon octet. By combining the u, d and s quarks, as they were so named, in every possible combination, eight different particles result. The same can be done with combining the anti-particles of u, d and s yielding the anti-particle octet to the baryon octet. Also, the meson octet, which contains both its particles and anti-particles, is formed by matching a quark with an anti-quark. In this model it remains to be seen whether the Eightfold Way is an accurate representation of the mesons since this quark model requires there to be nine mesons--three of which have Q=S=0.
Bibliography
Ne'eman, Yuval and Yoram Kirsh. The Particle Hunters. Cambridge: Cambridge University Press, 1986.
Griffiths, David. Introduction to Elementary Particles. New York: John Wiley & Sons, Inc., 1987
Ohanian, Hans C. Modern Physics. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1987.
Beiser, Arthur. Concepts of Modern Physics. New York: McGraw-Hill Book Company, 1987.