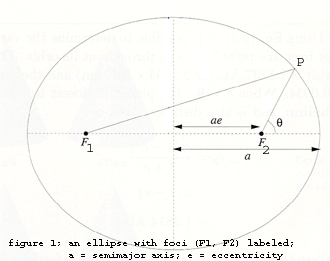
 longest axis ( =
major axis) of the ellipse.
longest axis ( =
major axis) of the ellipse.  compent of the
velocity vr
). Because these two components are perpendicular, they are
related to the orbit speed by the Pythagorean theorem:
compent of the
velocity vr
). Because these two components are perpendicular, they are
related to the orbit speed by the Pythagorean theorem: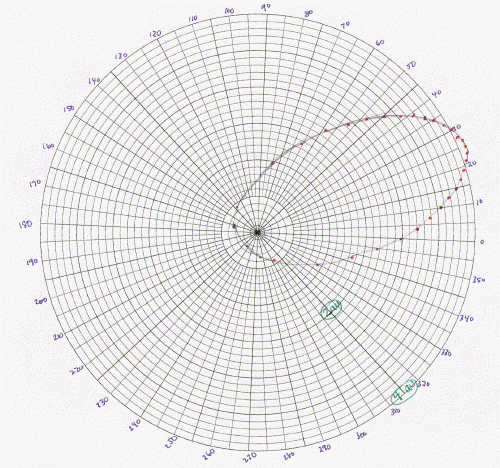 The orbit of comet Encke generated in the
manner
described is shown at the right. The red dots show the position
of the comet at monthly intervals. The sun is located at the black dot
at the center of the polar plot. Note the labels of 2 au and 4 au
radially.
The orbit of comet Encke generated in the
manner
described is shown at the right. The red dots show the position
of the comet at monthly intervals. The sun is located at the black dot
at the center of the polar plot. Note the labels of 2 au and 4 au
radially.