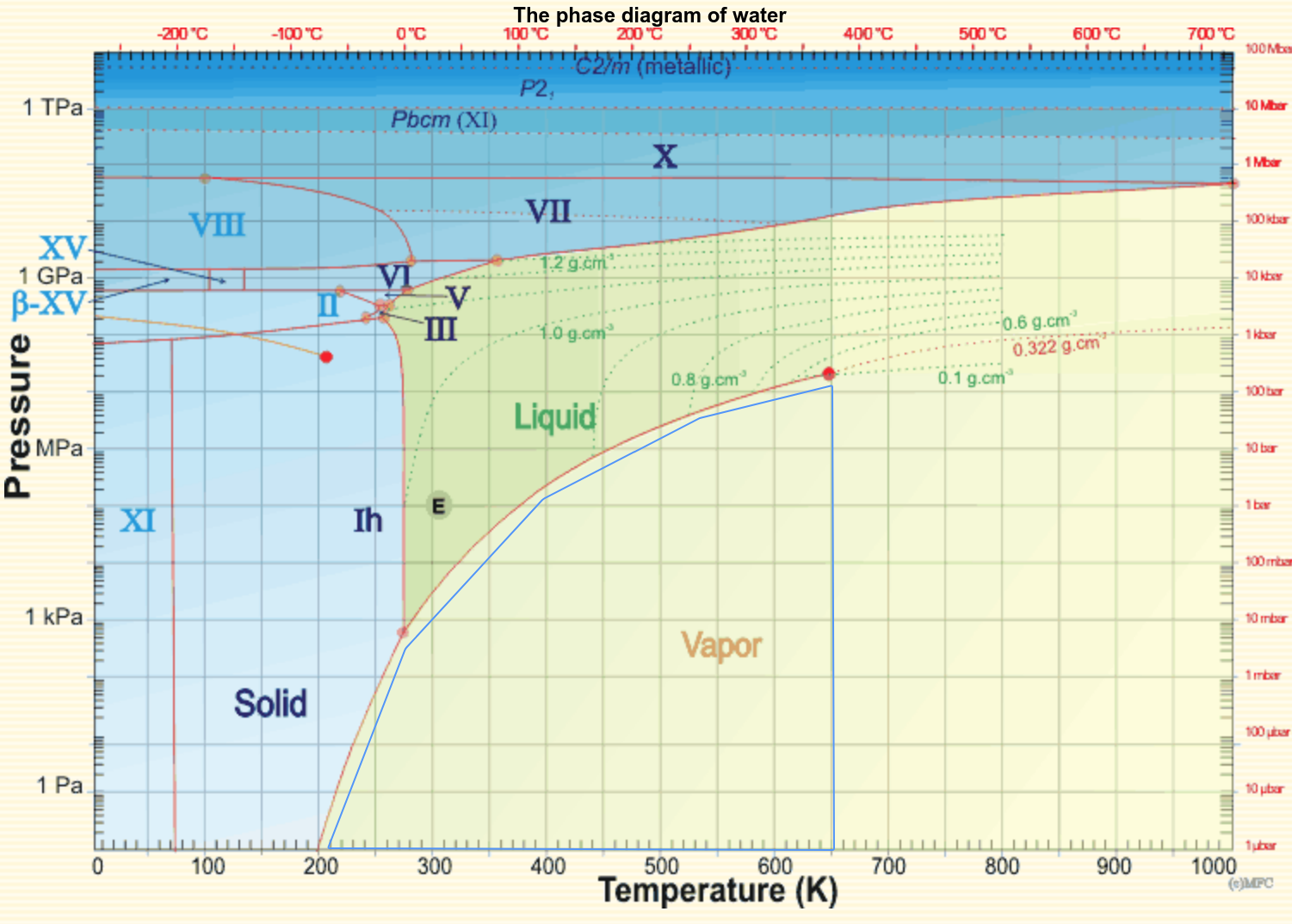
From the website Water Structure and Science by Martin Chaplin.

This phase diagram raises interesting questions: how do the phases differ from one another? For a given substance like water, is there a limit to how many phases can exist? What are the rules that govern how one phase changes into another phase as temperature and pressure are varied in tiny steps? In the figure you can see several so-called triple points (these are the lightly shaded orange circles) where three phases such as solid-liquid-vapor or solid-solid-liquid phases can coexist (water has ten triple points). Can a quadruple or higher-order point exist? A starting point for answering these questions is the observation that, in equilibrium, a phase line is determined by where the chemical potentials μ of the two phases are equal.
For many physicists, the most interesting feature of this phase diagram is not the diversity of phases but the remarkable behavior near the so-called called critical point at about the coordinate (Tc, pc) ≃ ( 650 K, 22 MPa) where the phase boundary between the liquid and vapor state suddenly ends at the red dot. What is not evident from this diagram is that the density of water ρliquid and the density of vapor (steam) ρvapor are unequal on either side of the liquid-vapor phase line, but the difference ρliquid - ρvapor of the densities decreases and goes to zero as the critical point is approached. Because the density difference is going to zero, you might think one could use Taylor-series expansions about the critical point to deduce the mathematical way that the quantity ρliquid - ρvapor and other quantities converge to zero or diverge to infinity. But experiments and simulations show that, say for fixed pressure and varying just the temperature, the difference in density goes to zero |ρliquid - ρvapor| → 0 as some power law |T - Tc|A with an exponent A that cannot be deduced from any kind of Taylor expansion. Further experiments show that different substances like CO2 have the same critical exponents and the convergence or divergence of quantities as they approach the liquid-vapor critical point seem to be independent of the substance.
Many other phase transitions such as the loss of magnetization of ferromagnetic iron as the temperature is slowly increased, or the onset of superconductivity (zero resistance) of a metal as the temperature of the metal is slowly decreased involve quantities that go to zero or diverge at the transition point and these quantities also behave mathematically as power laws with exponents that cannot be understood by Taylor expansions. Physics 763 will discuss some of the remarkable physics, experimental and theoretical, that finally clarified why there are universal classes of critical exponents that depend just on symmetry and dimensionality but not on the molecules making up a substance. The research led to several Nobel prizes in physics and the invention of the so-called renormalization group, a theoretical framework for studying phase transitions, problems in quantum field theory, and problems in nonequilibrium physics.
The study of phase transitions has proved to be extremely valuable for
many problems beyond equilibrium phase transitions. If we think of the
different phases that form from "structureless" vapor as a kind of
pattern formation (say through the formation of different crystalline
structures), phase transitions become an important conceptual and
technical metaphor for understanding how complex structure emerges
from simpler structure as some parameter is varied. Experiments and
theoretical work concerning phase transitions have strongly influenced
how people think about questions such as cosmology, nonequilibrium pattern
formation (say formation of cloud patterns or snowflakes), the
transition from inanimate to animate molecules (origin of life), the
formation of matter, stars, and galaxies from the superhot plasma of
the Big Bang, consciousness in brains (is this an abrupt transition as
brains become bigger?), and the properties of social, economic, and
computer networks.