Physics 212: Quantum Mechanics II
Spring Semester, 1999

Professor Henry Greenside

Welcome to the home page for Physics 212 which is the second half of Duke's year-long undergraduate sequence in nonrelativistic quantum mechanics. Continuing from Physics 211 in the fall semester, Physics 212 completes the foundation of quantum mechanics and applies this foundation to a wealth of scientific problems drawn from atomic physics, particle physics, nuclear physics, condensed-matter physics, astrophysics, and chemistry. Further information is available from the course syllabus .

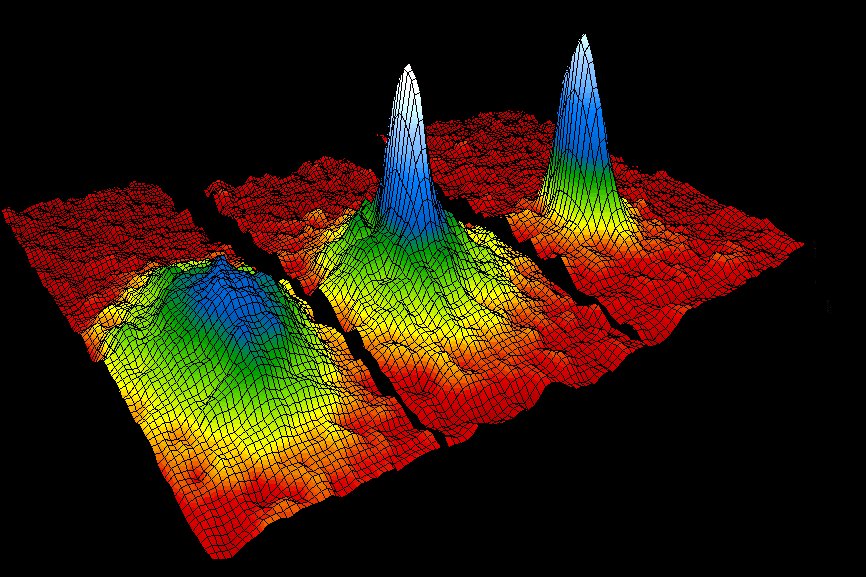
These false-color images display the velocity distribution of a cloud of rubidium atoms at (a) just before the appearance of the Bose-Einstein condensate, (b) just after the appearance of the condensate and (c) after further evaporation left a sample of nearly pure condensate. The field of view of each frame is 200 x 270 micrometers, and corresponds to the distance the atoms have moved in about 1/20 of a second. The color corresponds to the number of atoms at each velocity, with red being the fewest and white being the most. Areas appearing white and light blue indicate lower velocities.

Announcements:

• No announcments.

Class Participants:

Related links:

• syllabus,
• lectures,
• homeworks,
• miscellaneous.

Duke Links:

• Duke ACES course database.
• Duke Physics Challenges.
• Duke's Physics Department.

• Physics Focus    Easy-to-read brief summaries of recent Physical Review Letters.
• Physics News Update    Easy-to-read brief summaries of general advances in Physics, often with nice graphics.
• Physical Review Letters Online.    The premier physics journal for new important results.
• Physics Today    Monthly magazine of the American Physical Society.
• Science    The premier American journal for important results in all areas of science.
• Science News     Brief nontechnical discussions of recent advances in science.

• Bell Labs History Museum    See especially the quantum phone book link.
• IBM Physics Research.    Check especially the nanotechnology , material science , and STM (Scanning Tunneling Microscopy) Gallery links.

• Getting Started with LaTeX

Miscellaneous

• Flipping atoms fast.
• Measurement of vibrating chemical bond
• Nobel Prizes in Physics.
• Periodic Table.
• Writing the word "optics" on a hydrogen atom.

Other quantum courses

• MIT's Quantum Physics II
• MIT's Quantum Physics III

• Paul Adrien Maurice Dirac
• Albert Einstein
• Enrico Fermi
• Erwin Schrodinger
• Werner Heisenberg

• AIP list of quantum computing links.
• Neil Gershenfeld's quantum computation group
• Quantum computing tutorial
• Braunstein's quantum computation tutorial.
• Scientific American article on quantum computing.

Research groups:

• At Duke:
  • Professor Al Johnson's "Center for In Vivo Microscopy", using magnetic resonance imaging.
  • Professor John Simon's research group in chemistry.
  • TUNL: Triangle Nuclear Laboratories (TUNL).
• Ketterle MIT research group on Bose-Einstein condensation.

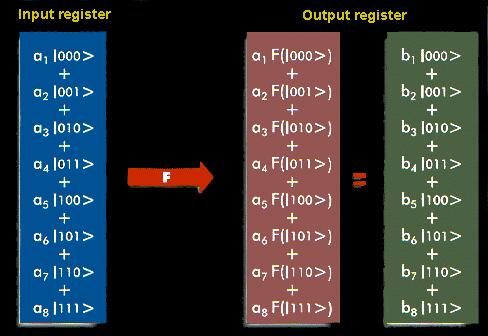
The ability for quantum mechanics to evolve kets in parallel using superposition offers the possibility for a new kind of computer that can solve certain problems far more efficiently than traditional digital computers. Quantum computation is an excellent example of how elementary non-relativistic quantum mechanics continues to find exciting and important new applications.. See the web page http://www.qubit.org/intros/comp/comp.html for an elementary tutorial on quantum computation.

Top of this page     Department of Physics