List of publications

Here is a summary of  activities in our research group.(updated May 14, 2015)

Former members of the research group (1997-2001):

Horst Meyer, professor - now emeritus.

Fang Zhong, research scientist - now staff member at the Jet Propulsion Laboratory, CalTech, Pasadena, CA.

Andrei B. Kogan, graduate student - now Associate Professor  in the Physics Department, U. of Cincinnati,
         Cincinnati, OH.

1) Equilibration dynamics of a pure fluid near the liquid-vapor critical point. (F.Zhong, A.B. Kogan and H. Meyer).

A fluid layer with fixed volume at the critical density is contained inside a cell bounded by two horizontal flat copper plates. We are investigating the density response inside this fluid to a perturbation by a temperature step or by an oscillatory temperature change of the copper boundary plates. This is an interesting problem that is relevant to experiments under microgravity where stratification is absent, and where the whole fluid layer can reach the critical point (Under the earth's gravity conditions, in presence of stratification, only a very small fraction of the fluid in the middle of the cell will remain at the critical density that permits the critical point to be realised). It turns out that both temperature and density equilibration are strongly influenced by a rapid perturbation through the fluid after the initial temperature step, called the "piston effect" that is a result of the strong density change at the boundary layers resulting from the diverging thermal expansion. The study of this effect is important because the thermal diffusivity slows down as the critical point is approached. Accounts have been published in Phys. Rev E 51,3223 (1995); E53, 5935 (1996), J. Low Temp. Phys. 108, 161 (1997). More recent experiments with a new cell, where equilibration and the effect of convection onset were studied, are published in an article by Kogan and Meyer, J. Low Temp. Phys. 112, 417 (1998).

2) Heat Transport in a pure fluid near the critical point: Steady state and relaxation dynamics in 3He.(F. Zhong and H. Meyer)

Near the critical point, where the compressibility diverges, density stratification in a fluid layer is introduced not only by the gravity field, but also by a heat flow through this layer. Both effects cause the measured thermal conductivity along the critical isochore to be smaller than predicted from mode-coupling and renormalization-group theories in zero gravity and in the limit of zero heat flow. Furthermore they shorten the thermal relaxation time compared with predictions. Calculations, done both in closed-form and also by numerical simulations have given quantitatively the effect from the stratification for both these effects on the thermal conductivity and relaxation time as a function of the heat current. They were compared with experiments and good agreement was obtained. A paper has appeared in the J. Low Temp. Phys. 114, 231 (1999)

3)Crossover behavior in 3-He and Xe near their liquid-vapor critical point. Work done in collaboration with E. Luijten (presently at the University of Illinois).

A detailed discussion is presented of the crossover from mean-field to Ising critical behavior upon approach of the critical point. By combining different sets of experimental data, we are able to cover an unusually large temperature range on either side of the critical temperature Tc. Below Tc, we can thus make an accurate comparison with a recent calculation (by Luijten) for the crossover of the coexistence curve. For the regime above Tc, an analysis of the compressibility demonstrates that the crossover regime in 3-He is unexpectedly widened by a subtle interplay between quantum and critical fluctuations. From the analysis, the corresponding Ginzburg numbers for each property are deduced. Also the first correction amplitudes for the confluent singularities are obtained from the fit of the data. The respective ratios of these numbers and those obtained for the coexistence curves for 3-He and Xe are discussed in terms of predictions by Bagnuls et al. E. Luijten and H. Meyer, Phys. Rev. E62,3257 (2000), H. Meyer, Proc. 2000 NASA/JPL Workshop on Fundamental Physics in Microgravity NASA Document D-21522(2001), cond-mat/0105333

4) Onset of convection in a Rayleigh-Benard cell in ³He along the critical isochore : steady-state and transients (A.Kogan and H. Meyer (experiments), collaboration with the group of A. Onuki and with G. Accary)

As the critical point is approached, fluids become very compressible. Then the onset of convection, calculated from the "Rayleigh" transition, is to take place at a temperature difference across the fluid layer that tends rapidly to zero. The increasing compressibility introduces another effect, the "adiabatic temperature gradient" ("Schwarzschild criterion"), which is usually unimportant in laboratory Rayleigh-Benard convection experiments. It is known by geophysicists because this effect is important in atmospheric phenomena for large air columns. However near the critical point this effect becomes important and dominates in fluid layers with conventional heights (order of 1 mm). We have observed this effect for 3- He, and as the temperature is increased away from the critical point, the Rayleigh condition for the convection onset eventually dominates. This is the first systematic study of the crossover from the Rayleigh to the Schwarzschild regime, and the experiments are in good agreement with the predictions. Another result of this study is the slope of the convective heat current versus Rayleigh number. This slope turns out to be independent of the compressibility for 3-He along the critical isochore, and to be the same as in much less compressible fluids such as liquid 4-He and water in R-B cells of similar aspect ratios.

Plots for the Nusselt- versus Rayleigh number are presented for early-stage convective turbulence. Data sets with Prandtl numbers up to about 100 follow approximately the 2/7 power law. However there are unexpected results for higher Pr numbers, the largest being approx. 590.

The evolution of the temporal transients in the temperature difference Delta T(t) across the fluid layer before the steady-state is reached has also been investigated in detail, and some quite unexpected effects were observed. Among them are damped oscillations of the temperature difference across the fluid layer that follow the first peak after starting the heat current. These oscillatory profiles have been compared with recent computer simulations by Chiwata & Onuki and Furukawa & Onuki(Kyoto University), which appeared in PRL'01 and in PR-E '02, and also with those by Amiroudine and Zappoli in PRL 90, 105303 (2003).

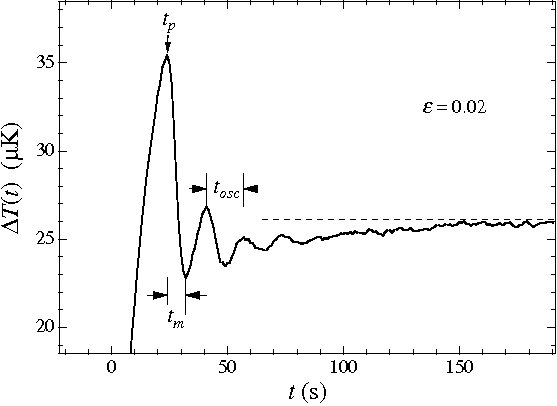
Fig.1 Selected portion of the temperature difference Delta T(t) across the fluid layer after the heat flow was started at time t=0. It defines the times t_p and t_osc. The relaxation time tau_asymp is obtained from an exponential fit of the observed recording to the asymptotic Delta T, shown by a straight horizontal dashed line.

    A detailed analysis has been made of certain characteristic times in the time profile of the temperature difference across the fluid layer mentioned above. These times are 1) the period of the damped oscillations t_osc, 2) the relaxation time tau_asymp with which the transient tends asymptotically to the steady state in an exponential way and 3) the time t_p from the heat flow onset to the peak of Delta T(t). These times are defined in the figure below what demonstrates the evolution of  Delta T(t) after the start of the heat flow

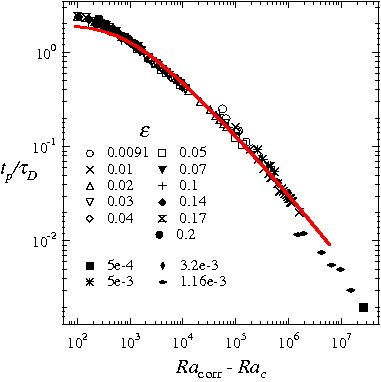
     For all the data at various reduced temperatures, the scaled ratios t_osc/tau_D, tau_asymp/tau_D and t_p/tau_D were found to fall each on one "universal" curve, when plotted versus the Rayleigh number. Here tau_D  is the diffusion relaxation time which is a function of L the height of the fluid layer (0.1 cm in our experiment), and D the thermal diffusion constant as mesured in separate experiments.
( Phys. Rev. Lett 82, 4635 (1999), Physica 284, 208 (2000), Phys Rev.E.63 056310 (2001), cond-mat/0209495, Phys Rev.E.66 056310 (2002) and in Physica B329-333, 114(2003).

    Comparison of the numerical simulations by A. Furukawa and A. Onuki with experimental data showed good agreement for the scaling of the steady state convection current and of t(osc) versus the Rayleigh number, but systematic discrepancies for t(p), where t(p) from simulation is larger than from experiments, indicating that the onset of convection in simulations is delayed in time in comparison with experiments (Furukawa, Meyer, Onuki and Kogan,(PR E 68 056309 (2003)).

    Introduction of temperature perturbation with a lateral periodicity of 2L into the simulations has shown that the onset of convection occurs significantly earlier, hence gives a lower t(p), and for a given amplitude brings experiment and simulations into near agreement. (Furukawa, Meyer and Onuki (PR E 71 067301 (2005).

a)"Equilibration and Other Dynamic Properties of Fluids near the Liquid-Vapor Critical Point" by H. Meyer and F. Zhong, Comptes Rendus de l'Academie des Sciences-Mecanique,332, 327 (2004)

b) "Time scaling in the convection onset of a supercritical fluid, by H. Meyer and G. Accary, Actes XIXème CFM 2009, Marseille article #1325 ISSN 0395 5437 (2009) [pdf]
 

  8) Invited Presentations at "March"meetings of the American Physical Society:
 
 a) "Fritz London's Legacy at Duke University" in "Low Temperature Physics: A Historical Perspective, Session U5, March 16, 2006,  http://www.phy.duke.edu/history/DistinguishedFaculty/WilliamFairbank/Londonlegacy.pdf

b) "Van Vleck and the magnetic susceptibilities of gaseous molecules" in "J.H. Van Vleck: Quantum theory and Magnetism" Session L8, March 22, 2011, http://www.phy.duke.edu/~hm/vanVleck/